Triangulation이란 무엇인가?
이번 글에서는
Triangulation
에 대하여 살펴보겠습니다.
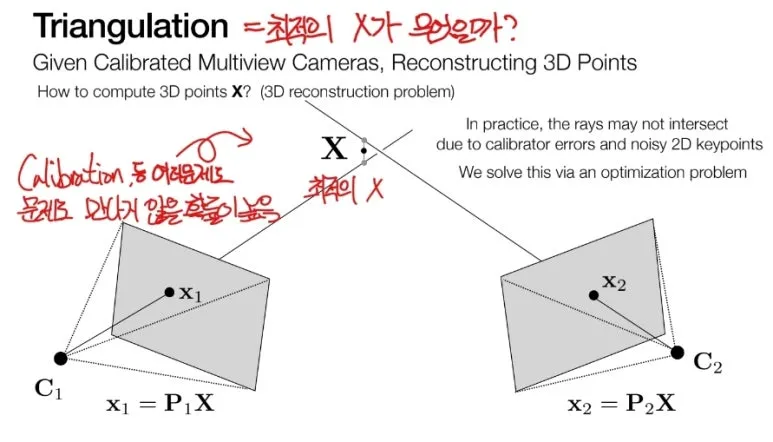
3D 에서 정말 중요한 Triangulation 은
Calibration 이 된 여러 카메라로 부터
3D Points 를 Reconstruction 하는 방법입니다.
우리는 3D point 를 복원하는 것이
목적이기 때문에
Depth 정보도 알아야 하므로,
하나의 카메라로는 불가능합니다.
Homogeneous 좌표와 외적 조건의 활용

우리는 Homogeneous coordinate 표현으로
3D 포인트가 2D 포인트로 프로젝션
되는 식을 적을 수 있습니다.
여기서, 2 개가 Up-to-scale 이라는 것은
두 벡터가 같은 방향을 바라보고 있으므로,
외적의 값이 0 을 의미합니다.
외적 = 0 을 이용하여
식을 만들어
Triangulation 을
풀어보겠습니다.
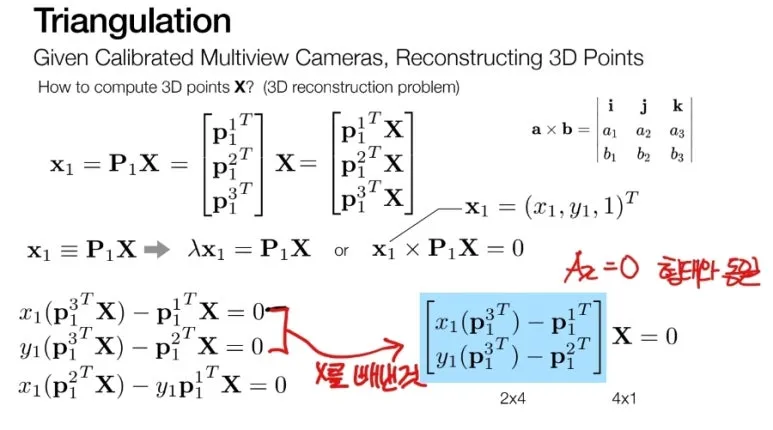
외적 = 0 을 이용하여
왼쪽 하단의 식 3개를
구할 수 있으며,
이를 잘 정리하여
오른쪽 하단의 식
2개를 구할 수 있습니다.
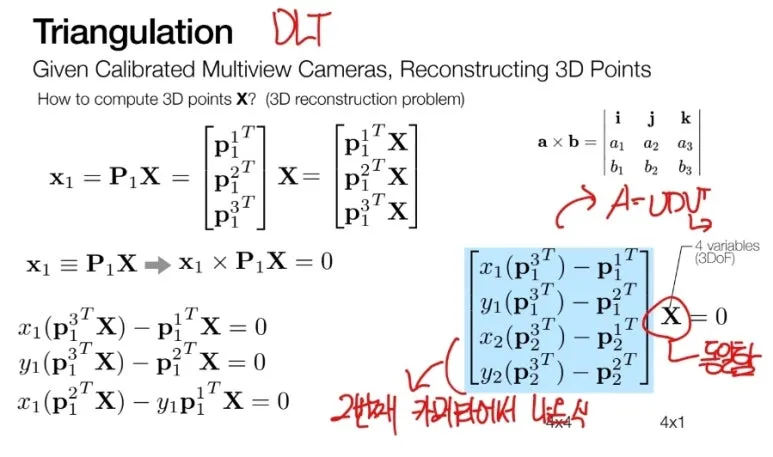
이 과정을 다른 카메라에도
똑같이 적용하여 식을 추출합니다.
이렇게 나온 식들을 모아서
DLT 로 문제를 풀게 됩니다.
Geometric Error 해결 방법
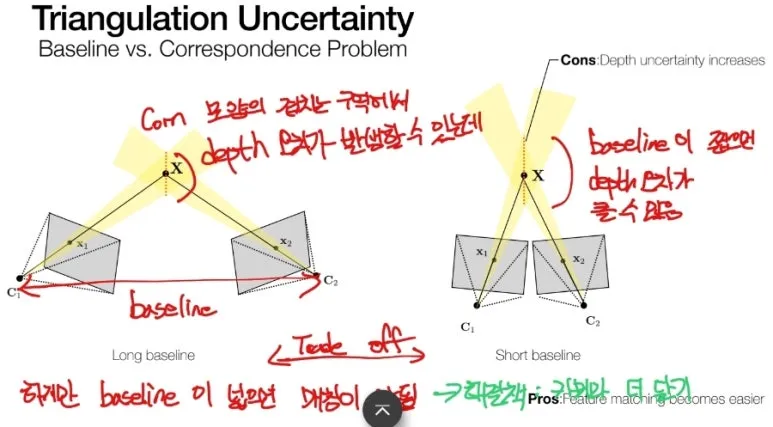
실제로 사용할 때는,
2D point 에 Backprojection 된 Line 2개가
서로 교차할 확률은 거의 없습니다.
어디선가 에러가 있기 때문에,
살짝 씩 벗어나게 됩니다.
정말 이상적인 경우에는
교차하겠지만요.
또한 두 개의 카메라의 Baseline 이
크게 되면 Depth 오류 영역이
줄어들긴 하지만,
각 카메라로 촬영한 이미지가
많이 다르기 때문에,
대응점을 찾기 힘들다는
단점이 있습니다.
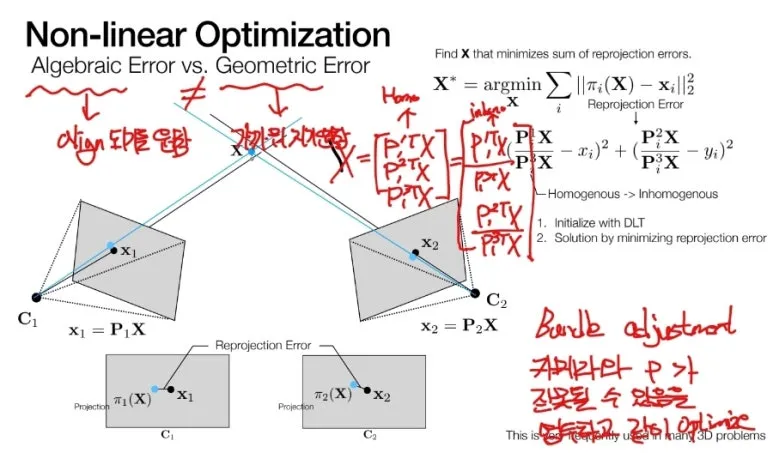
우리는 외적 = 0 으로 부터의 식으로
Algebric 하게 Triangulation
문제를 풀었습니다.
| 항목 | Algebraic Triangulation | Geometric Triangulation (Reprojection 기반) |
|---|---|---|
| 계산 방식 | 외적 = 0 기반 선형 방정식(DLT) | 이미지상의 Reprojection error 최소화 |
| 사용 목적 | 빠르고 직관적인 초기 추정 | 정밀도 높은 최적화 결과 얻기 |
| 오차 고려 여부 | 없음 (노이즈 민감) | 있음 (노이즈/오차 최소화 반영) |
| 계산 비용 | 낮음 (선형 계산) | 높음 (비선형 최적화 필요) |
| Bundle Adjustment 사용 가능 | 불필요하거나 추가 가능 | 필수 (카메라 파라미터도 함께 최적화) |
| 결과 정확도 | 중간~보통 | 높음 |
하지만, 여러가지 에러들 때문에
차이가 발생하고,
이 차이를 최소화 하기 위해
각 이미지에 프로젝션 된
실제 포인트의 위치와
대수적으로 계산을 통하여 얻은
포인트 위치 사이의 거리를
최소화하는 방법을 통해서
(= Reprojection error)
더욱 정확한 답을 찾아냅니다.
여기서 Budnle adjustment 라는 것은
카메라 파라미터도 틀릴 수 있다고 가정하고,
Reprojection loss 를
줄이기 위해서,
이 파라미터 들도
최적화를 같이 진행하는 것을 말합니다.
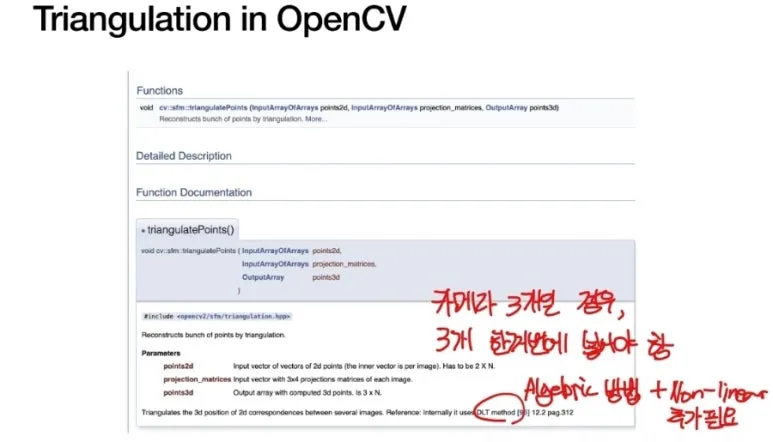
Triangulation 방법도
OpenCV 에 잘 정리된
코드가 있습니다.
주의할 사항이 하나 있습니다.
만약 카메라 여러개를 사용했다면,
한번에 DLT 에 적용해서
풀어야 모든 카메라
projection 을 만족하는
3D point 를 복원할 수 있습니다.
그런 건 난 잘 모르겠고,
Triangulation 은
여러 카메라로 부터
3D 위치 복원하는 방법
참고자료
Slide credit : Joo Hanbyul
https://homes.cs.washington.edu/~seitz/talks/3Dhistory.pdf
