기저벡터

행렬(Matrix)의 의미, Linear Transformation으로 쉽게 이해하기

by
행렬7

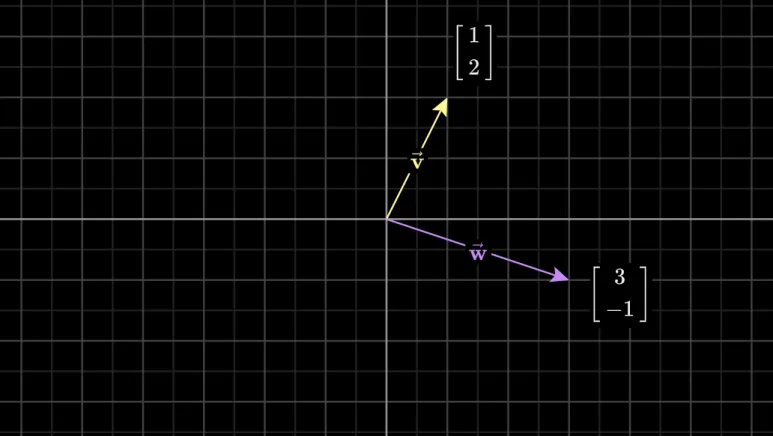
선형 변환이란 무엇인가? 이전 글에서 살펴본 선형 변환을 어떻게 수치적으로 기술할까요? 일단 Input vecor 와 Output vector 를 표기할 수 있어야 합니다. 기저(Basis)와 벡터 표현 2차원 공간 위에서 벡터를 표현하기 위해 두 기저벡터를 사용하겠습니다. [-1,2] 라는 벡터를 기저 벡터로 표현한 뒤 Linear Transformation (선형 변환) 해보겠습니다. 선형 변환과 격자선의 관계 ​ 선형 변환은 평행하고 균등하게 … Read more

기저벡터(Basis Vector)란? i hat, j hat 으로 벡터 공간을 이해하자

by
임의의 기저벡터1

기저벡터(Basis Vector)의 개념 xy 좌표계에는 두 개의 특수벡터가 있습니다. ​ 오른쪽 x축으로 1만큼 향하는 i hat 벡터 위 y축으로 1만큼 향하는 j hat 벡터 벡터의 선형 결합 표현 우리는 이 두 벡터를 이용하여 어떠한 벡터를 스케일된 두 벡터의 합 으로 표현할 수 있습니다. ​ 이 특별한 두 벡터 i hat, j hat 을 Basis vector … Read more