Structure from Motion(SfM)이란?
이번 글에서는
3D 기초 중에서 가장 중요한
Structure from Motion
에 대하여 살펴보겠습니다.
여태까지 다뤘던 여러가지 내용이
결합하여 매우 실용적으로 작동합니다.
가장 먼저 제안된 SfM 이 있지만,
여러가지 제약이 많았습니다.
저희는 요즘 사용되고 있는
더 발전된 SfM 을
집중적으로 살펴보겠습니다.

Input 으로는 동일한 무언가를
촬영한 이미지들이 들어가게 됩니다.
Output 으로는 Point Cloud 와
각 카메라의 파라미터를
알 수 있게 됩니다.
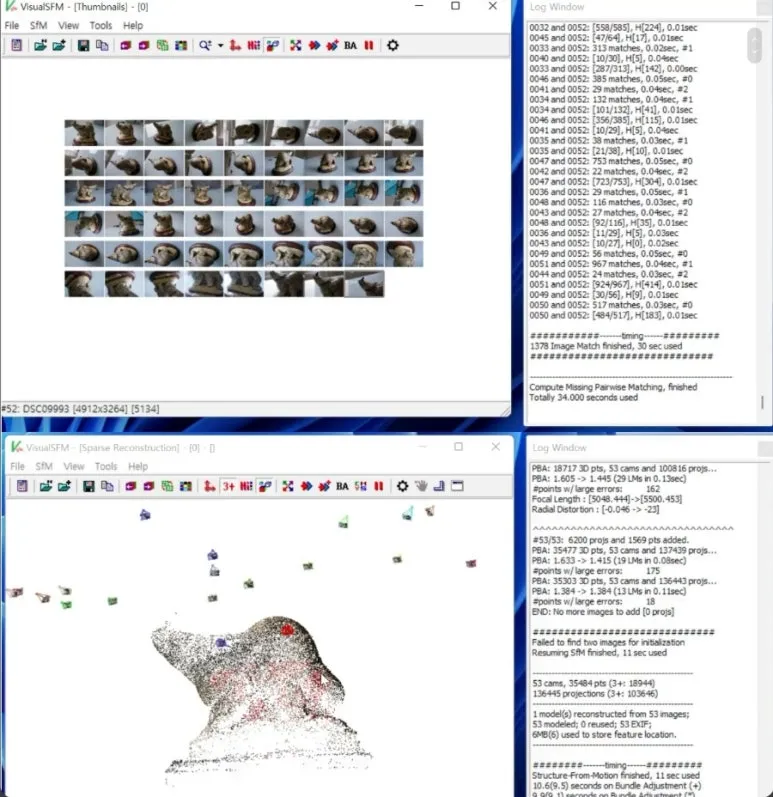
이미 오픈소스로 최적화까지 되서
신뢰성 있게 작동하는
VisualSfM 과 COLMAP 을
통하여 직접 사용해 볼 수 있습니다.
SfM 전체 과정

이미지들을 촬영한 카메라의
내부 파라미터인 K 는
주어져 있다고 가정하는데,
없어도 Optimization 을 통해
자동적으로 구해지므로
신경쓰지 않으셔도 됩니다.
우선, 이미지들에서
Feature 를 추출하겠습니다.
가장 먼저 SIFT 를
적용해 볼 수 있습니다.
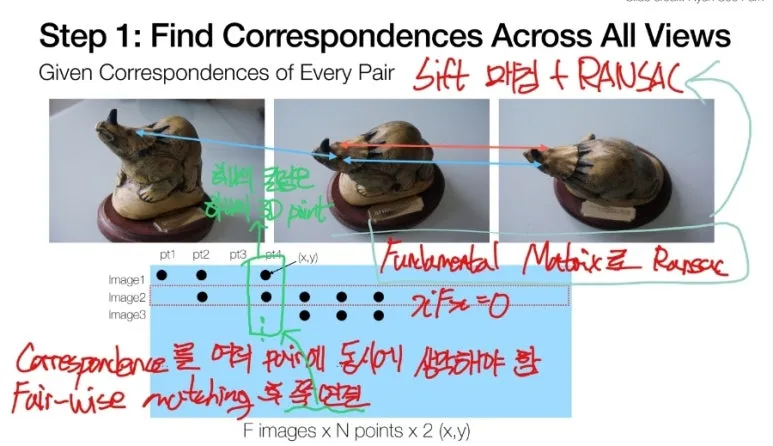
각 이미지에서 SIFT feature 를
추출한 다음에 Matrix 를
만들어서 정리합니다.
각 행은 1개의 이미지를 의미하며,
각 열은 공통된 feature 를 의미합니다.
하나의 열에서 1번 이미지와
2번 이미지가 포함된다면,
두 이미지는 해당되는
공통되는 Feature 를
가지고 있습니다.
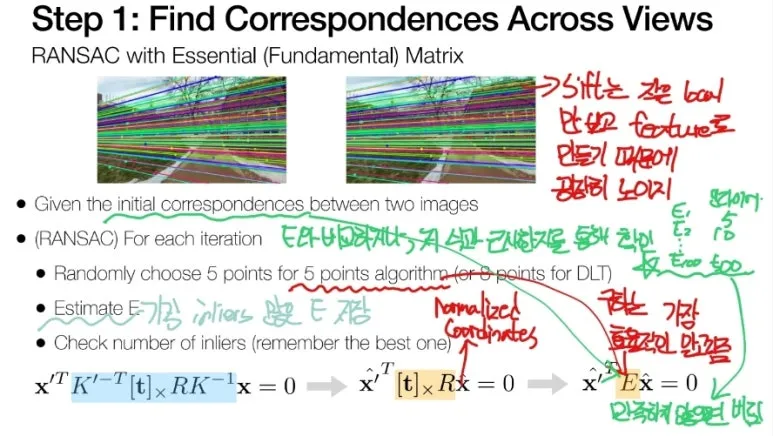
그런데, Feature 추출은
정확하지 않으므로,
RANSAC 과 같은
이상치 제거가 필요합니다.
두 이미지 사이의 대응점을
가장 많이 가지는 Fundamental Matrix 를 찾습니다.
Essential Matrix 는 F를 알고 있을 경우,
Fundamental Matrix 에서
더 DoF 를 줄일 수 있습니다.
Fundamental Matrix 는
8-point algorithm 을 통해서
Essential Matrix 는
5-point algorithm 을 통해서
구할 수 있습니다.
자세한건 이전에 관련 내용으로
작성한 글이 있으니
참고하시면 좋을 듯 합니다.

우리는 지금 2장을 이용하여
적절한 대응점들을 찾았습니다
. 이제 이것을 이용하여
뼈대를 구축하고,
살을 붙여가는
느낌으로 진행할 것입니다.
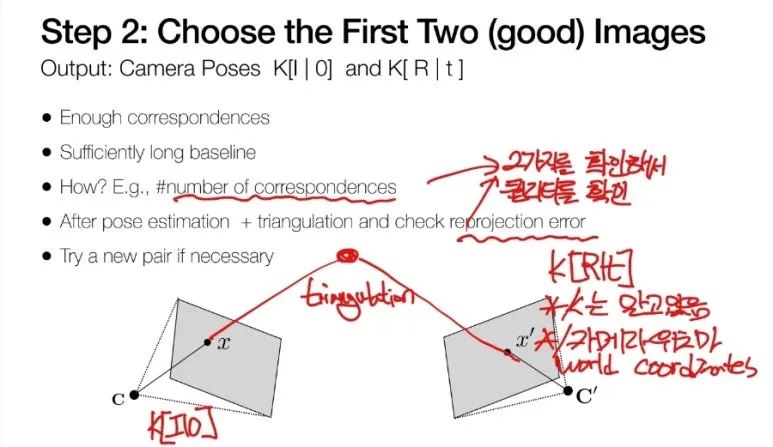
뼈대를 구축한다는 게
무슨 뜻인지 자세히 살펴보겠습니다.
처음의 2장의 이미지를
선택하는 것이 성능에 매우
큰 영향을 끼치게 됩니다.
가장 많은 대응점을 가지고 있는
두 이미지를 이용하는 것이
가장 튼튼한 뼈대를
만들 수 있습니다.

카메라 포즈를 설정합니다.
두 이미지 중에 한 장을 기준으로
(Camera coordinate = World coordinate) 만듭니다.
다른 한장은 기준으로 부터의
R,t 로 위치를 설정합니다.
R,t 는 우리가 구한 Essential Matrix 를
분해하여 얻을 수 있습니다.

하지만 4가지의 해답이 나오며,
그 중 진짜 답은 1개 이므로
모두 직접 적용해보고,
적절한 R,t 를 판단하게 됩니다.
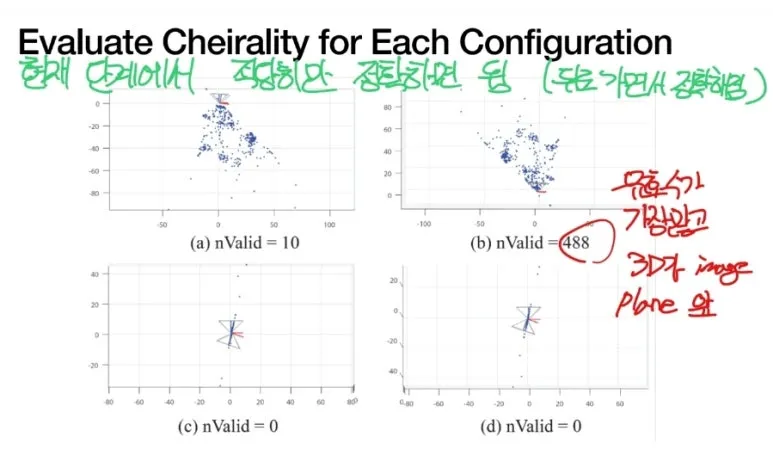
3D cloud point 가
Image plane 앞에 위치하게 되면
옳은 R,t 라고 판단하게 됩니다.

이제 우리는 2개의 카메라 포즈와
3D cloud point 들을 가지고 있습니다.
가장 대응점이 많은
두 장을 이용하여 만들었으니
꽤 신뢰성이 있다고 볼 수 있습니다.
이제 여기에 다른 이미지들을
한장 한장 붙여나가겠습니다.
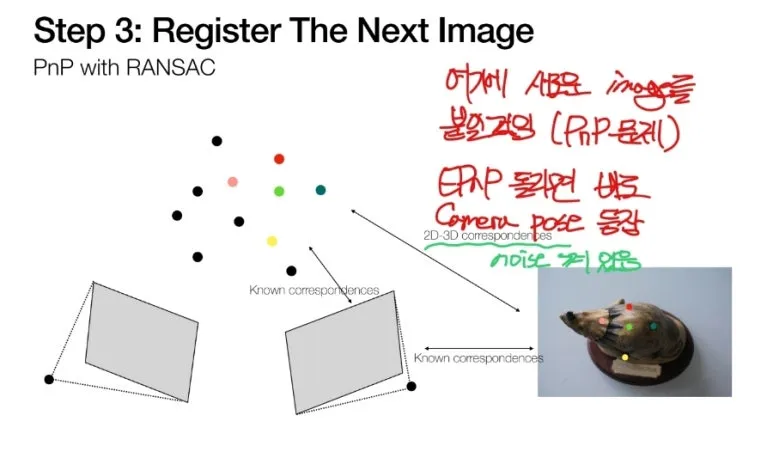
EPnP algorithm 을 통해
새로운 이미지의 R,t 를 구할 수 있습니다.

이렇게 새로운 카메라를 붙이면,
새로운 대응점들이 생기게 됩니다.
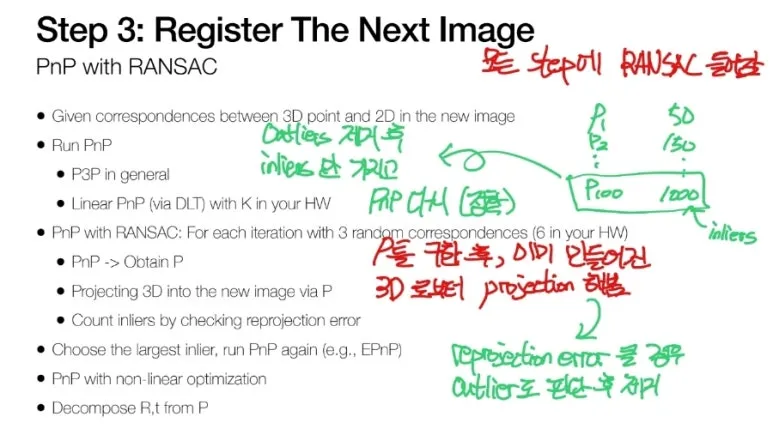
우리가 구한 새로운 이미지의 카메라 포즈가
더욱 정확하게 만들기 위해서,
EPnP 로 구한 카메라 포즈를 이용하여
Reprojection error 를 통하여
RANSAC 을 진행하게 됩니다.
이렇게 이상치들을 제거해주는
작업을 계속 섞어가며
진행하게 됩니다.

새로운 카메라를 붙였으니,
이제 이 이미지에서의 feature 들과
기존 이미지들의 feature 사이에
새로운 공통되는 대응점들이 생겼습니다.
따라서,
새로운 3D cloud point 들을
만들어야 합니다.
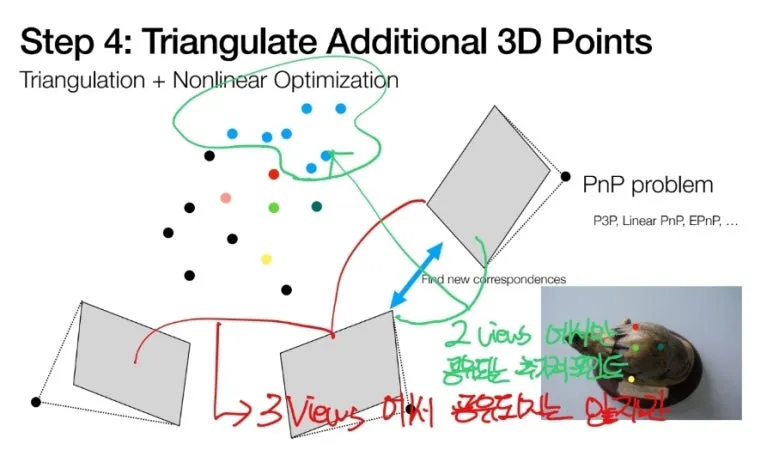
반드시 기존에 있는
이미지 모두와 대응될
필요가 없습니다.
어차피 3D point 는
Triangulation 을 통해서
2장의 이미지만 있어도
만들 수 있기 때문에
따로 따로 진행할 수 있습니다.
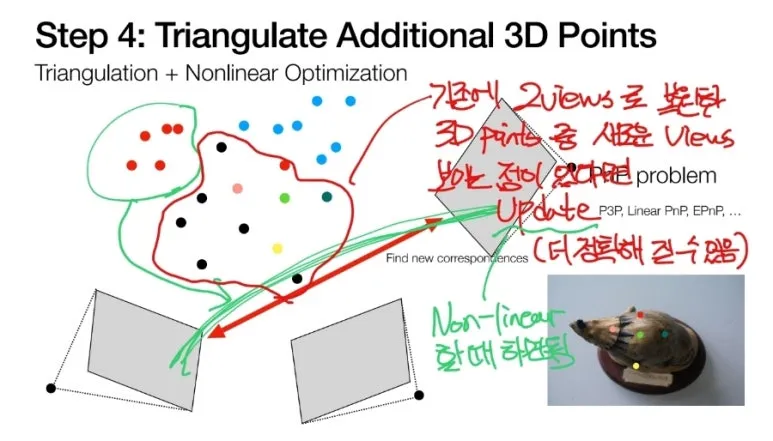
물론, 기존의 이미지들 사이의
대응점이 새로운 이미지에
동일하게 있을 수 있습니다.
이럴 경우,
update 를 진행하여 더욱
정확하게 만들 수 있습니다.

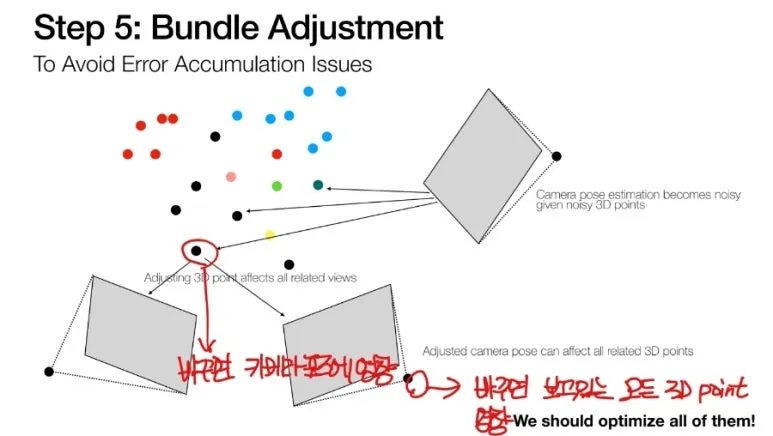
우리는 이미지를 붙일 때마다,
Bundle adjustment 를 진행해 주게 됩니다.
즉, 지금까지의 카메라 위치들과
3D point 들을 이용하여
전체 데이터를 수정하는 작업입니다.
Gradient-descent 방식의
Optimization 이기 때문에,
데이터가 커질 수록
시간이 많이 소요됩니다.
여러 카메라가 붙고,
3D Cloud point 가 많아진다면,
100 번마다 1번
이런식으로 조절 하게 됩니다.
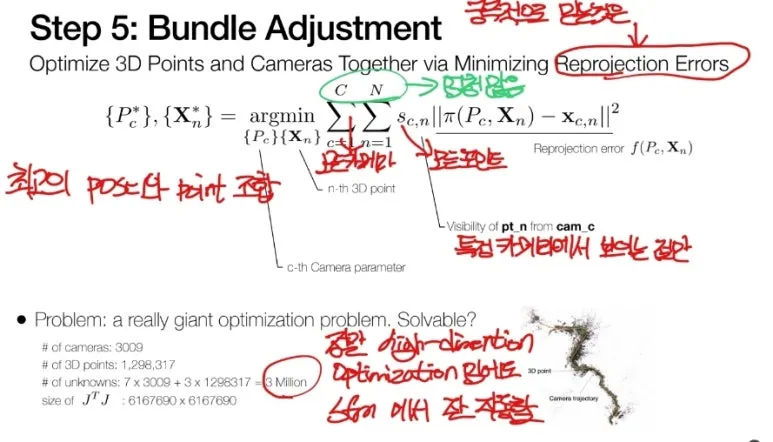
모든 카메라 포즈와,
Cloud point 가 움직일 수 있고,
Visibility (1,0) 으로 (해당 카메라에서 보이는 Cloud point 만)
계산하게 됩니다.
우리가 원하는 것은 Reprojection error 만
감소되면 됩니다.
데이터가 정말 정말 고차원 인데
어떻게 Optimization 이
작동하나 의문이 듭니다.
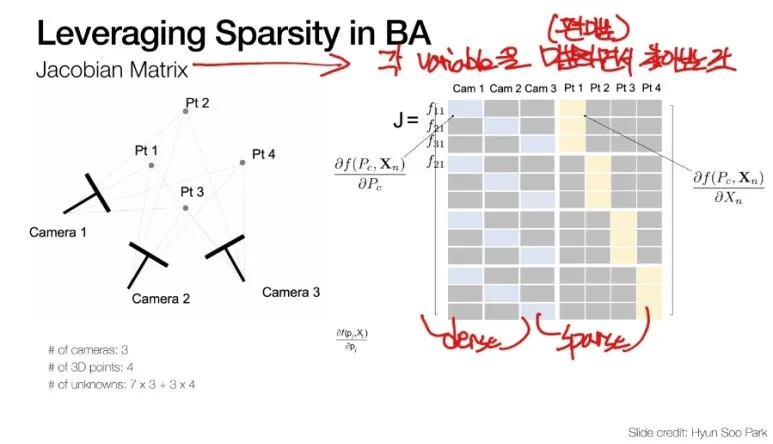
Jacobian Matrix 는
가능한 모든 변수들을 미분하면서
변화량을 찾아보는 것 입니다.
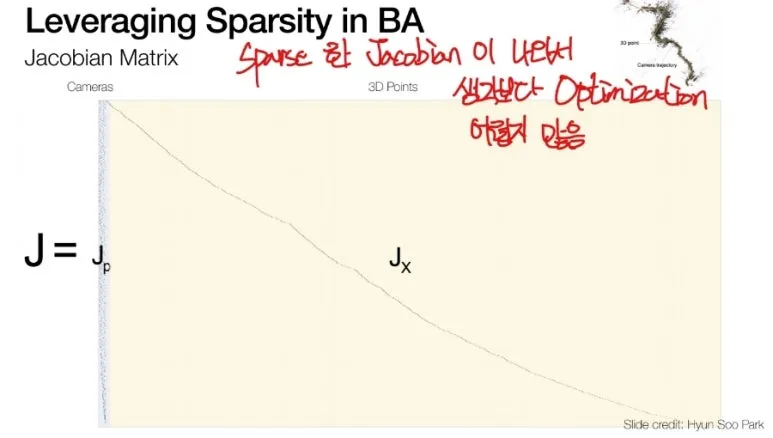
실제로 자코비안을 구해보면
카메라와 관련되서는
상당히 dense 하지만,
3D point 에 대해서는
sparse 한 것을 볼 수 있습니다.

즉, 중요한 부분이 매우 한정적이기
때문에 우리는 Optimization 을
할 수 있습니다.

SfM 의 정말 매력적인 부분은
정말 다 해준다는 겁니다.
처음에 언급했던 Intrinsic parameter K,
Distortion parameter 까지도
한번에 얻을 수 있습니다.
더 자세한 내용은 여기를
참고하시면 좋을 듯 합니다.
그런 건 난 잘 모르겠고,
SfM 은 이미지 여러 장으로
3D cloud point 와
카메라 포즈를 얻는 방법
참고자료
Slide credit : Joo Hanbyul
https://homes.cs.washington.edu/~seitz/talks/3Dhistory.pdf
