확률의 정의: P(A) = 사건 A가 일어날 확률
이번 글에서는 정말 중요한
확률에 대해 알아보겠습니다.

우리는 Sample space 와 Event에
대한 튼튼한 개념이 있습니다.
Sample space(전체 경우의 수)와
내가 정의한 Event(사건)를
만족하는 수를
알 수 있다면
P(A) = Event 가
일어날 확률을
구할 수 있습니다.
P() = 확률
A = 내가 정의한 Event
사실 수학에서 무언가를
정의하기 위해서 만족해야
되는 조건들이 있습니다.
저는 그런 것들 잘 모르고,
어지러워서 제 글에서는
본질적인 핵심만 다룰 예정입니다.
저의 머리는 섭섭하게도
그런 거 다 기억할 수 없습니다.
주사위 예시로 살펴보는 확률 계산
우리는 계속해서 주사위를
예시로 보고 있습니다.
주사위 1개를 던져서 나올 수 있는
Sample space의 경우의 수는 6입니다.

S = {1,2,3,4,5,6}
Event (A)를
주사위를 던진 결과가 6이
나올 때라고 정의하면

전체 6개의 경우의 수
중 1개뿐입니다.
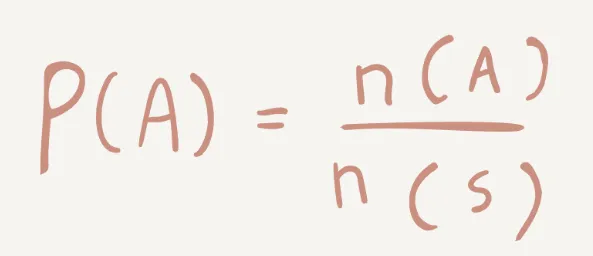
그러면 확률은 1/6 이 됩니다.
확률은 왜 0~1 사이의 값일까?
우리는 Event 가 Sample space의
부분 집합임을 살펴봤습니다.
그러면 결괏값은 무조건
0~1 사이의 값이 되어야 합니다.
(분모가 전체 집합,
분자가 부분 집합이므로)
이 간단한 내용을 암기만 하고
내용을 나아가도 헷갈리는 부분을
확연히 줄일 수 있습니다.
그런 건 난 잘 모르겠고,
Probability (확률)은
어떤 실험 (Sample space)의
모든 경우의 수에 대해
특정 사건이 발생하는 비율
참고자료
https://www.kdnuggets.com/2023/02/importance-probability-data-science.html
