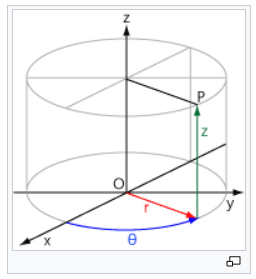
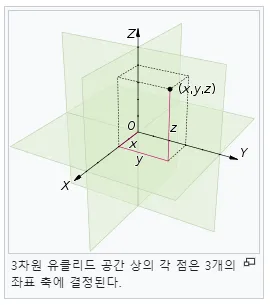
원통 좌표계(Cylindrical Coordinates)란? 거리, 각도, 높이로 3차원 공간을 표현하는 방법
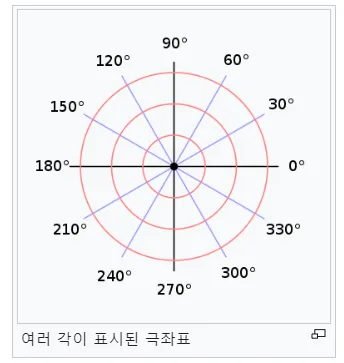
원통 좌표계란 무엇인가? 이번 글에서는 원통 좌표계에 대해 알아보겠습니다. 이번 정의도 상당히 직관적입니다. 우리가 이전에 살펴본 극 좌표계는 데카르트 좌표계의 2차원을 그저 다르게 표현하는 것이었죠. 데카르트 좌표계에서 원통 좌표계로 변환 원통 좌표계는 데카르트 좌표계의 3차원을 다르게 표현합니다. 데카르트 좌표계에서 2차원은 극 좌표계로 3차원은 원통 좌표계로 변환이 가능하네요. 공통점이 있죠? 각도가 들어간다는 것 … 더 읽기