선형 결합이란?
여러 벡터를 이용하여
새로운 벡터를 만드는 것을
Linear combination (선형 결합)
이라고 합니다.
만약 Basis vector (기저 벡터) 를 이용하여
선형 결합으로 새로운 벡터를 만든다면
기저 벡터가 정의하는 공간의
모든 차원의 벡터를 만들 수 있습니다.
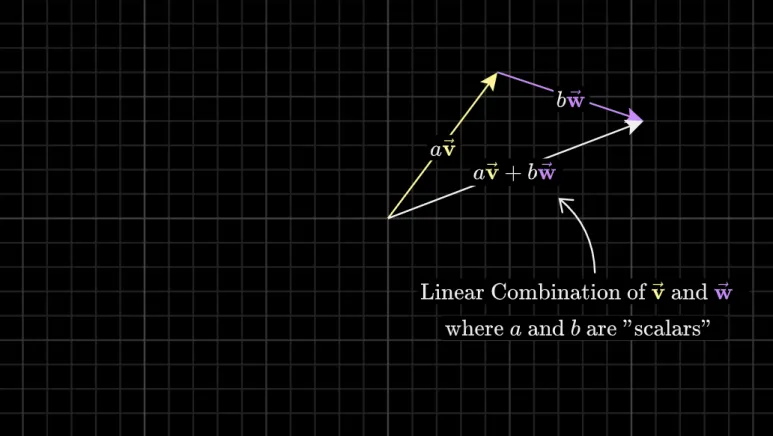
즉, 어느 공간에 벡터가 있다면
그 벡터는 해당 공간의 기저 벡터의
선형결합으로 정의할 수 있습니다.
‘선형(Linear)’의 의미는 무엇인가
두 벡터를 합쳐서 하나의 벡터를
만드니까 결합은 알겠는데,
Linear (선형) 은 무슨 의미일까요??
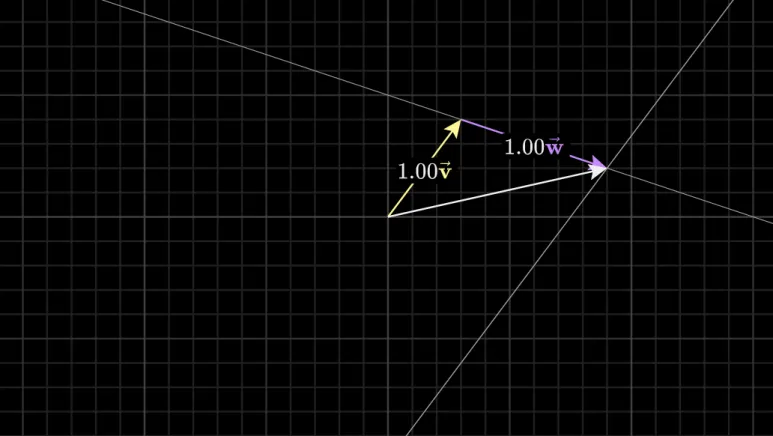
우리가 한쪽 스칼라를 고정하고,
다른 스칼라만 변경할경우
그림처럼 선을 그리게됩니다.
(참조에 동영상을 보시면 직관적입니다.)
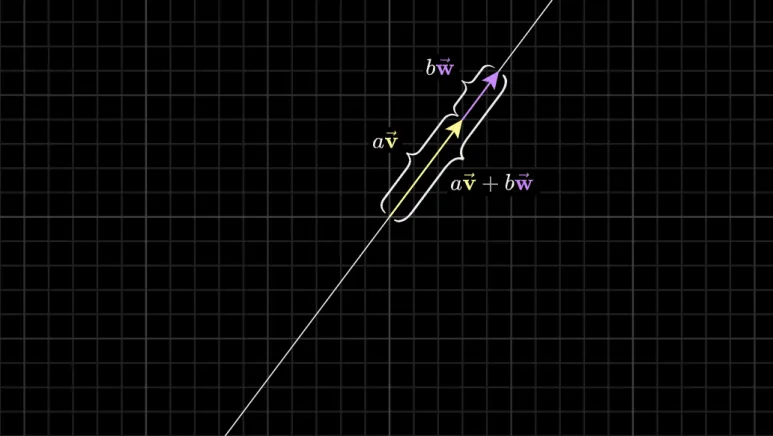
만약 선형결합을 하기 위한 벡터가
위 그림처럼 정렬되면 새로운 벡터는
동일한 선상 위에만 존재하게 됩니다.

벡터가 모두 영벡터인 경우는
뭘 할 껀덕지도 없습니다.
Span이란? 벡터로 만들어지는 공간
주어진 벡터의 선형결합으로
만들 수 있는 모든 벡터의 집합을
주어진 벡터의 Span(생성) 이라고 부릅니다.
(저는 벡터의 집합 보다 공간이라고
받아들이는 것이 직관적이라 생각합니다.)
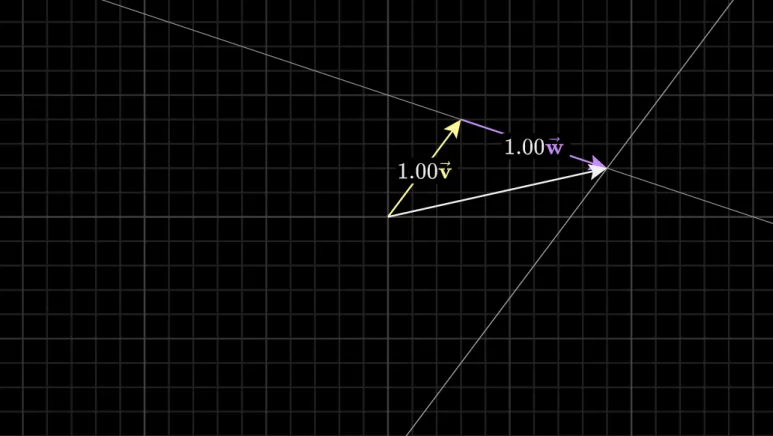
이러한 벡터의 선형결합으로
만들 수 있는 새로운 벡터는
2차원 공간위의 모든 벡터이지만,
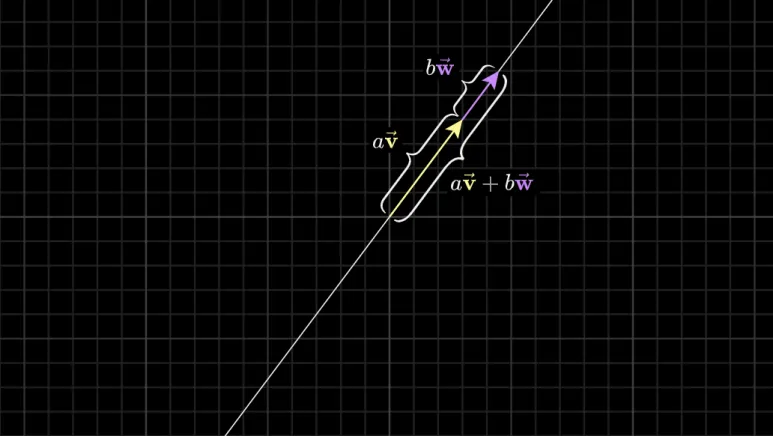
이런 벡터의 선형결합으로 만들 수 있는
새로운 벡터는 1차원 특정 선 위의
모든 벡터입니다.
즉, Span 은 주어진 벡터를 이용하여
벡터의 덧셈과 스칼라배, 이 두 연산 만을
이용하여 만들 수 있는 벡터는 무엇이 있는가?
묻는 것과 같습니다.
2차원과 3차원에서의 Span 직관적으로 이해하기
제가 벡터의 집합을
공간으로 이해하는 것이
직관적이라고 설명했었습니다.
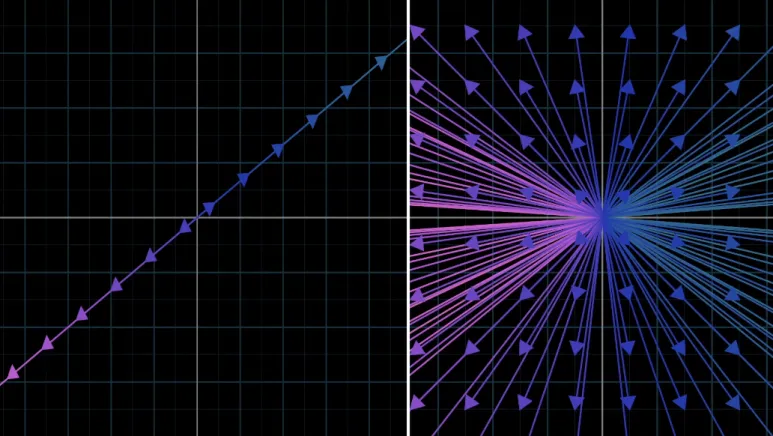
그림과 같이 많은 벡터의 집합을
생각하는 것은 복잡해집니다.
하나의 벡터 자체를 생각할 때는
화살표로 생각하고,
이와 같이 벡터의 집합을 다룰 때,
각 벡터를 한 점 (벡터의 머리)로
표현하는 것이 일반적입니다.
이렇게 표현하면
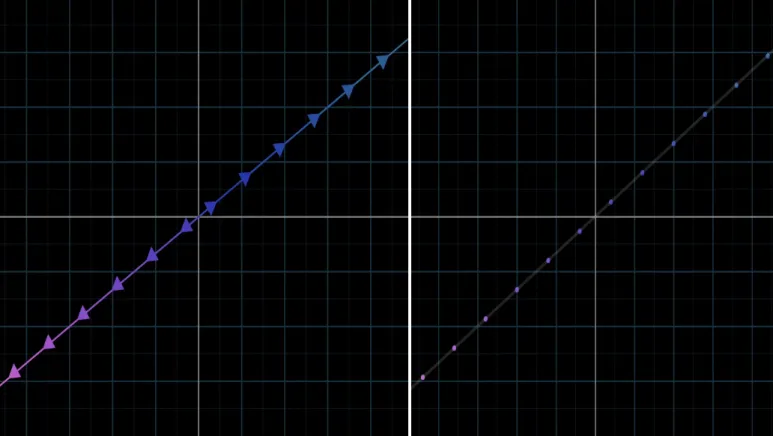
이러한 벡터의 집한은
한 선으로 표현할 수 있고
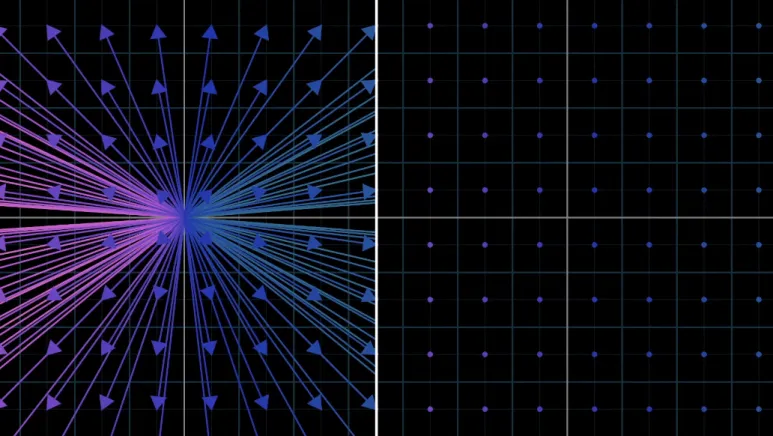
이러한 벡터의 집합은 2차원 공간의
무한한 평면으로 생각할 수 있습니다.
3차원에서 생각해보겠습니다.
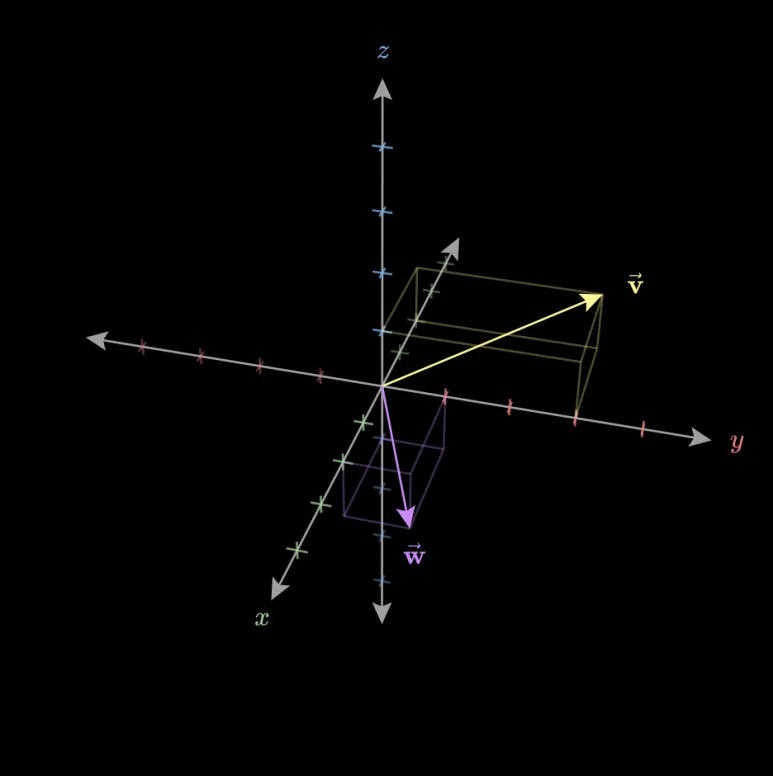
3차원 안 에서의 위 그림의
두 벡터의 Span 은 무엇일까요?
두 벡터의 모든 선형결합의 집합입니다.

이렇게 만든 집합은 3차원 안에서
원점을 지나는 2D plane 을 그리게 됩니다.
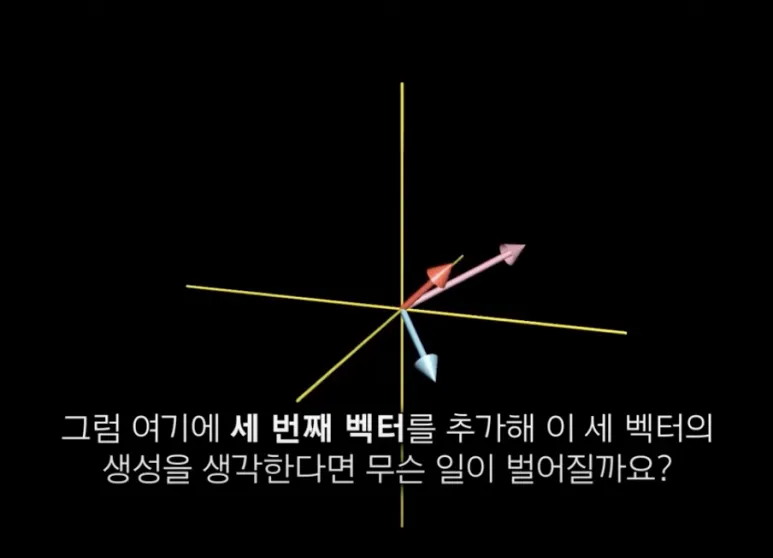
하나의 벡터를 추가한 뒤 Span 을 구해보겠습니다.
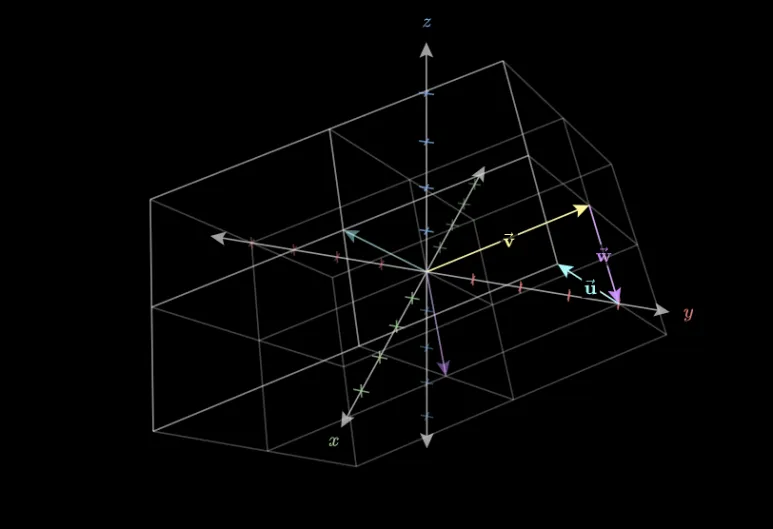
무한한 3차원 공간의 새로운 벡터의
집합을 생성할 수 있습니다.
선형 종속(Linearly Dependent) vs 선형 독립(Linearly Independent)
주의할 점이 있습니다.
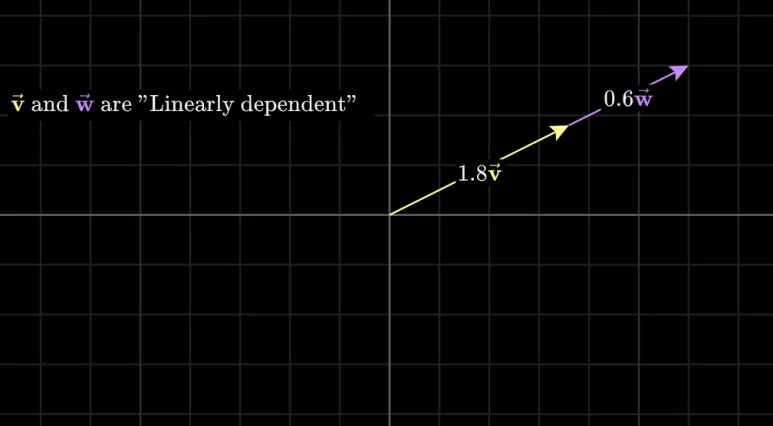
만약 새로운 3번째 벡터가
기존 다른 두 벡터의 생성에 놓이는 경우나,
그림과 같이 한 직선 상에 놓인
벡터가 있다면 벡터가 중복되므로
Span 의 차원에 영향을 끼치지 못하고
이러한 경우를
Linearly dependent(선형 종속) 라고 표현합니다.
즉, 선형 종속은 Span 의 축소 없이 벡터들
중 하나를 제거해도 되는 경우를 말합니다.
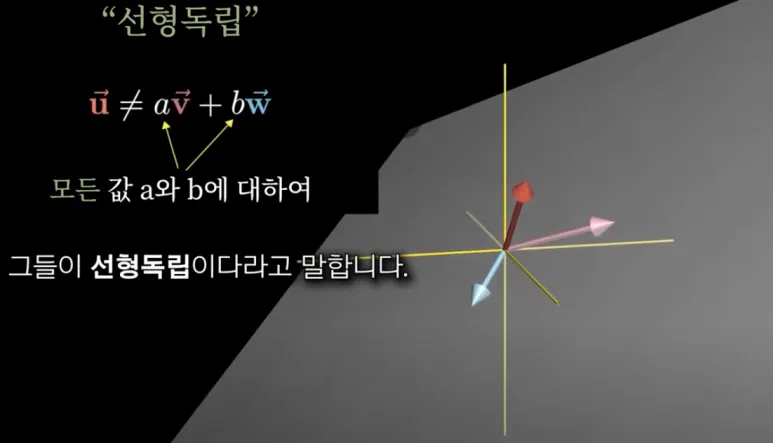
이렇게 모든 벡터가 Span(생성)에 다른 차원을
구성한다면 이 벡터들을
Linearly independent(선형 독립) 이라고 부릅니다.
