Homography란 무엇인가?
이번 글에서는
Homography
에 대하여 살펴보겠습니다.
Homography 의
사전적 정의를
살펴보겠습니다.

뭐라고 하는지는 잘 모르겠지만,
투영 기하학 안에서
발생하는 것 같습니다.
직관적으로 예시를
먼저 살펴보겠습니다.


우리가 스포츠 경기를 시청하다 보면
분명히 CG 같은데 굉장히 자연스러운
효과가 들어간 장면들을
볼 때가 있습니다.
이러한 것들을 적용하기 위해
사용되는 것이 Homography 입니다.
우리는 Projective Geometry (= 투영 기하학) 이
무엇인지 살펴봤었습니다.
다시 한번 살펴보면,
Geometry 는 어떠한 변형을 했을 때,
변하지 않는 성질에 대한
공부를 의미합니다.
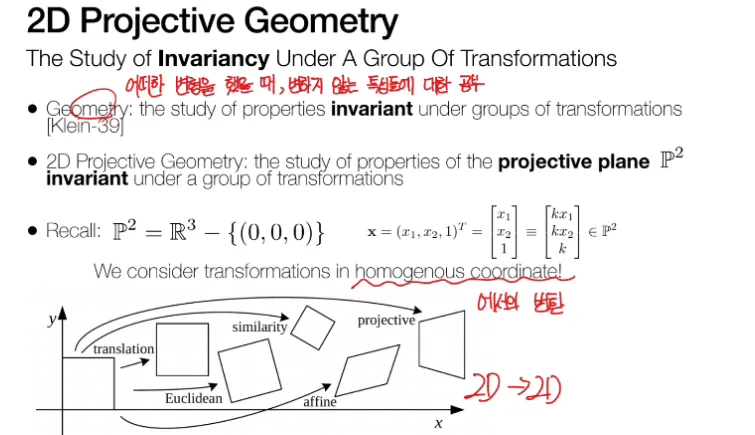
Projective 는 우리가 알고
있는 세상이 아니라,
카메라를 통해 본 세상과 같이
투영된 세상입니다.
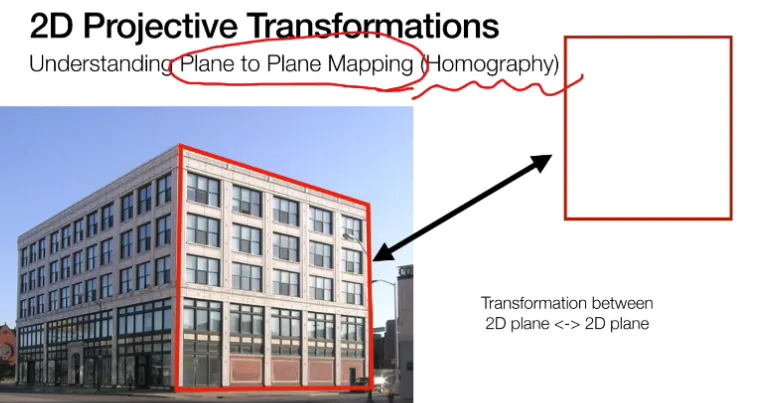
투영된 공간에서 2D (= Plane)의 변환을
다루는 것이 Homograpy 입니다.
Homography의 수학적 정의와 DoF
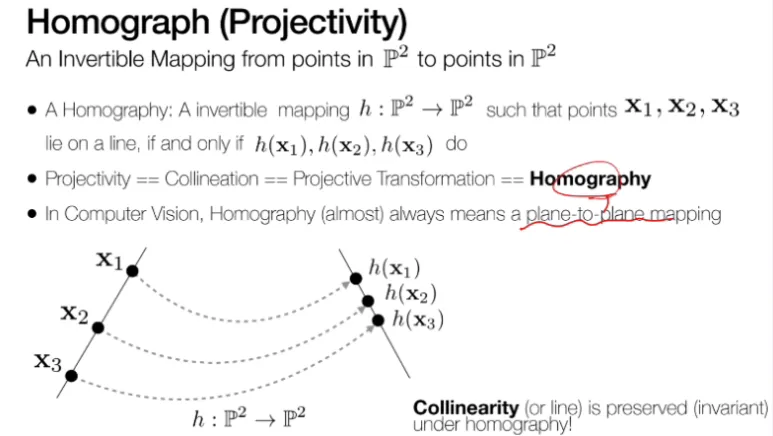
Homography 안에서도
다양한 변환으로 나눌 수 있으며,
각 변환마다 다른 성질을
가지고 있습니다.

Hmography 는 3×3 행렬로 정의되며,
8 DoF 를 가지면서
Invertible 하다는 특징이 있습니다.
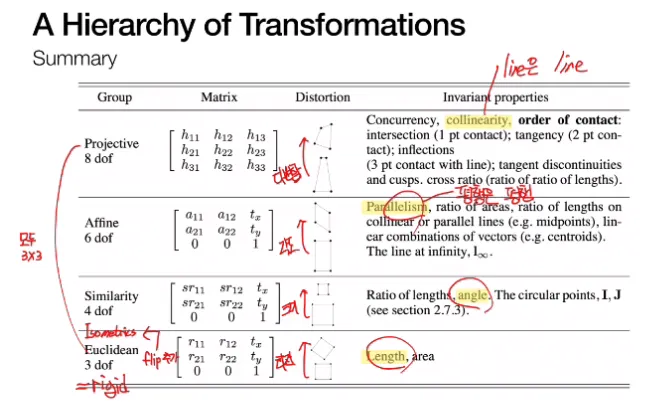
Homography 안에서도 다양한 변환으로
쪼갤 수 있는데 이 모든 변환은
Homography (=Projective Transformation) 의
부분집합에 해당됩니다.
각각의 변환마다 3×3 행렬에서
어느 부분이 추가되어
DoF 가 늘어나는지,
변환마다 절대 변하지 않는
속성은 무엇인지를
파악하는 것이 중요합니다.
Homography 변환의 계층 구조
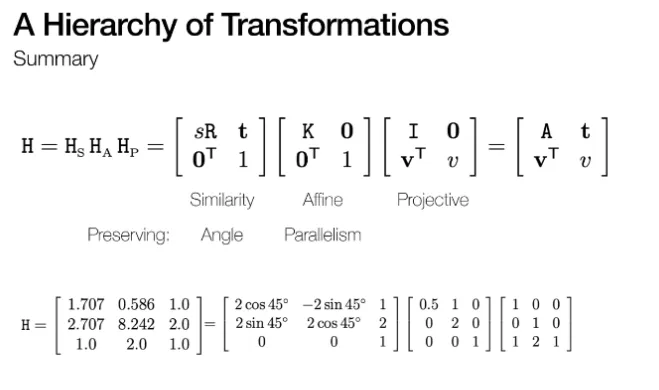
이러한 Transformations 들은
계층적으로 구성되어 있습니다.
우리가 처음에 본 예시처럼
사진에서 공통된 부분을
찾아서 이어 붙이거나,
특수 효과를 자연스럽게 넣기 위해서는
어떤 변환을 적용해야 하는지를 찾아서,
해당 변환에 맞는 DoF 만큼의
Correspondence (대응점) 을 찾아야 합니다.
이 대응점이 변수를 풀 수 있는 식을
만들기 때문에 최소한 변수 수만큼은
대응점이 필요하게 됩니다.
Homography가 아닌 변환은?
그러면 Homography 가 아닌 것은 뭐가 있을까요?
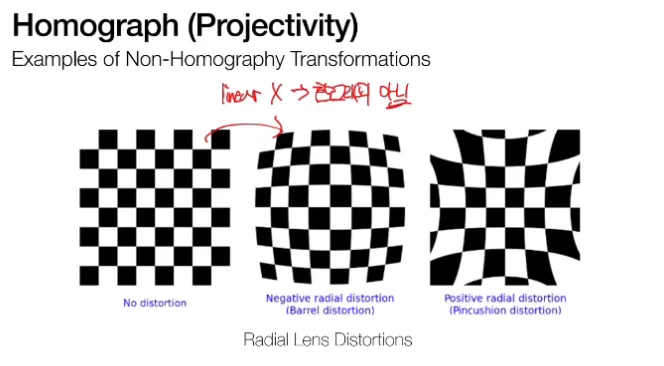
간단하게 예시만 보면,
우리가 어떤 렌즈를 통해서 빛이 왜곡되서
모양이 변하는 것과 같은 현상은
변형 후 선분이 직선이 아니라
휘어지게 되기 때문에
Homgraphy 가 아닙니다.
한 가지 의문이 더 들 수 있습니다.
투영된 공간에서 2차원만 다루는데,
3차원은 없는건가?
정답은 ‘있습니다.’
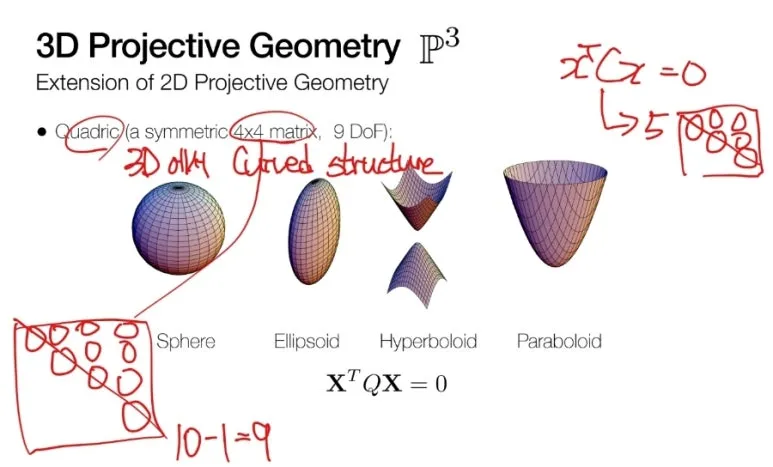
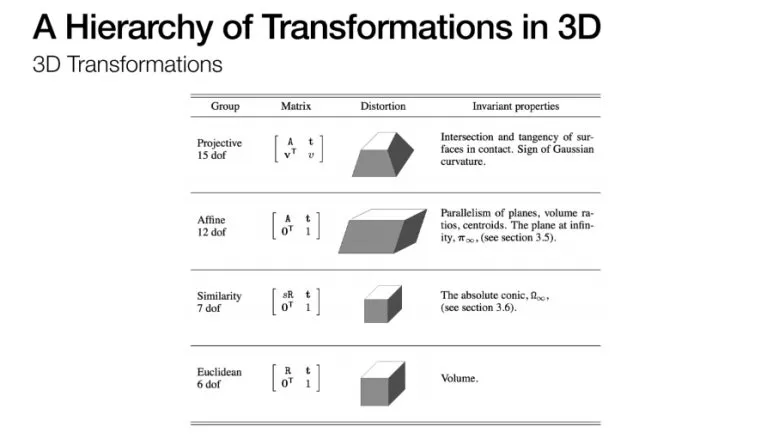
하지만.. 어려우니 그만 알아보겠습니다.
그런 건 난 잘 모르겠고,
Homography (= 2D Projective Transformation)는
Plane to Plane mapping
참고자료
Slide credit : Joo Hanbyul
https://homes.cs.washington.edu/~seitz/talks/3Dhistory.pdf
