Epipolar Geometry란 무엇인가?
이번 글에서는
Epipolar Geometry
에 대하여 살펴보겠습니다.
Epipolar Geometry 는 카메라 2대 사이의
geometry property 를 의미합니다.
역시 직관적이지 않습니다.
바로 예를 보자면,
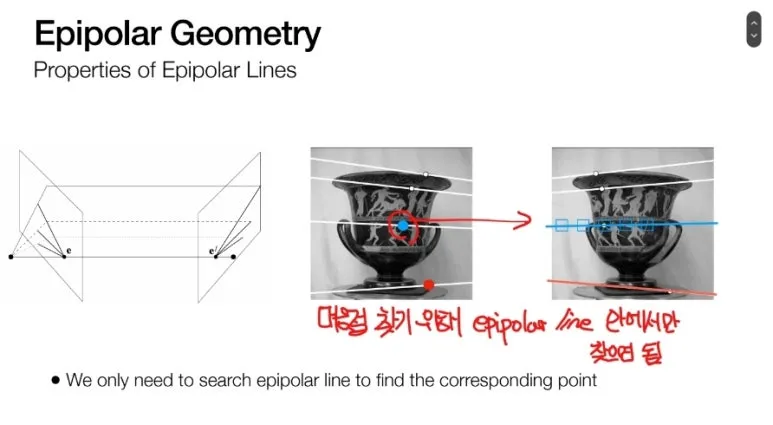
그림과 같이 서로 다른 2대의
카메라에서 찍은 사진 2장이 있습니다.
한쪽 사진에서 어느 선분
위에 있는 어느 점과
대응되는 다른 사진에서의 점은
반드시 특정 선분 위에
위치해야 합니다.
이 말은 즉슨,
대응점을 찾기 위해
찾아야 하는 범위가
확 줄은 것과 같습니다.
천천히 살펴보겠습니다.
Epipole 과 Epipolar Line 개념
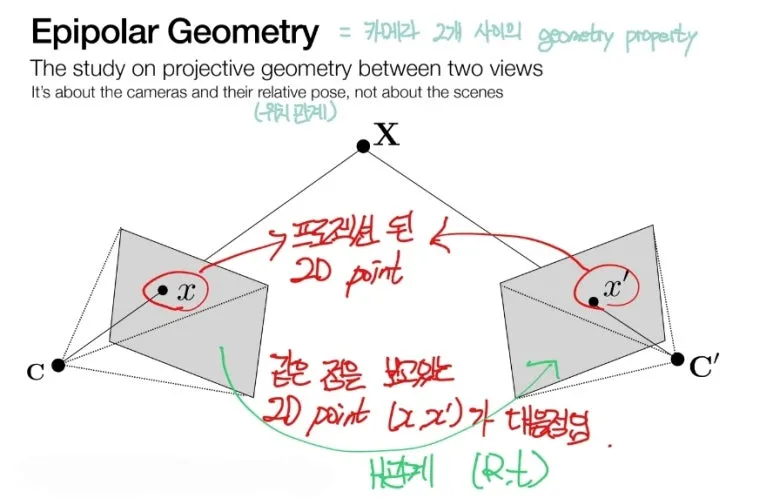
두 개의 카메라가
동일한 3D 좌표 X 를
촬영하고 있습니다.
각 카메라가 찍은 이미지에는
프로젝션 된 2D point (x,x’) 가
각 이미지 위에 보이게 됩니다.
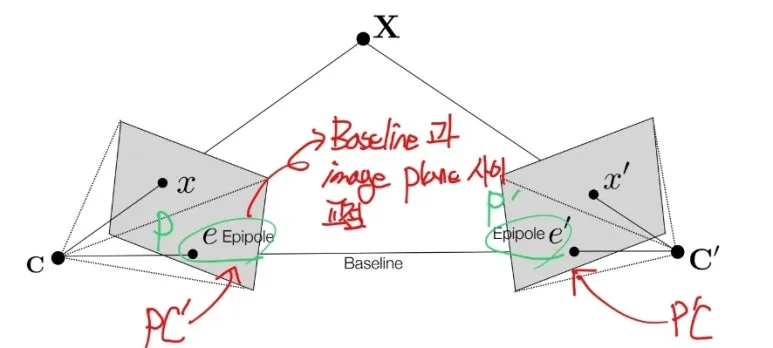
한 카메라의 중심(C) 를
다른 카메라 이미지 평면에 투영된 점을
Epipole 이라고 합니다.
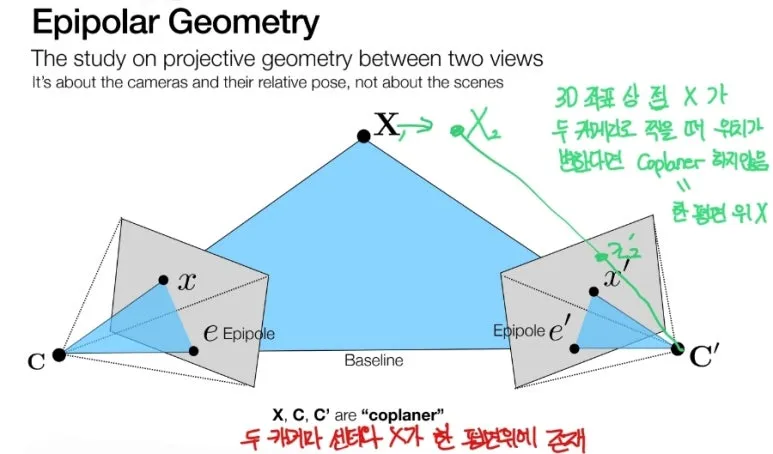
2개의 카메라의 센터와
1개의 3D 좌표 X 를 이용하여
총 3개의 점을 연결하여
평면을 만들 수 있습니다.
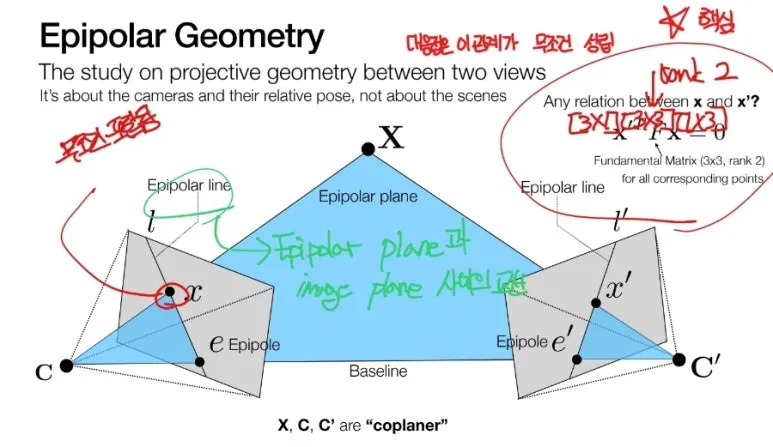
각 이미지에는
프로젝션 된 2D X 포인트와
Epipole 이 있습니다.
이 두 점을 이은 선분을
Epipolar line 이라고 합니다.
정리해 보겠습니다.
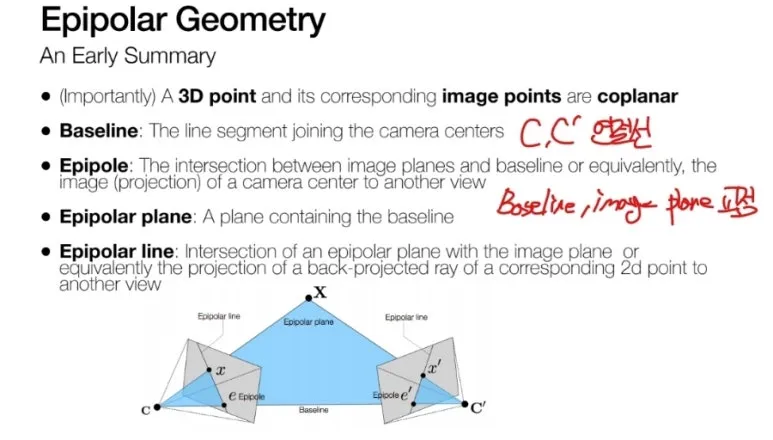
Epipolar Geometry 가 가지는 특성
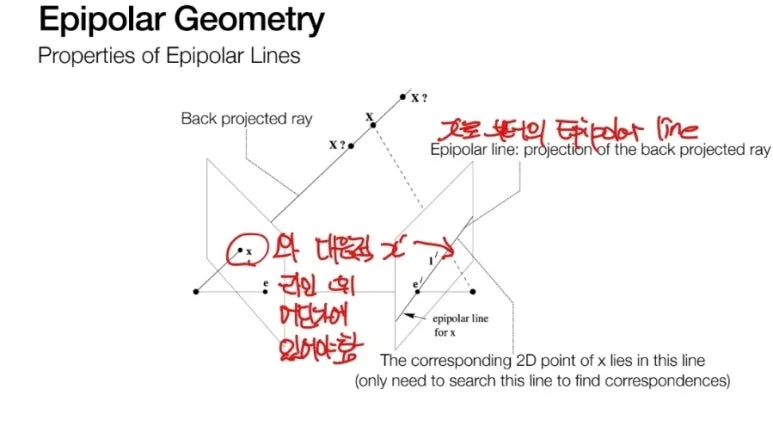
Epipolar Geometry 는
동일한 3D 좌표 X 를
프로젝션 한 x 는
다른 이미지의
Epipolar line 위에
반드시 존재해야 하는
특성을 갖습니다.
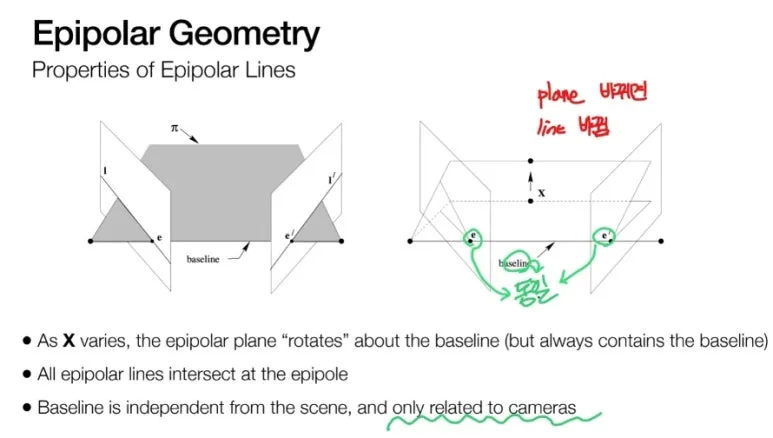
3D 좌표 X 가 움직여서
다른 Epipolar Plane 으로 바뀌면
Epipolar Line 도 변하게 됩니다.
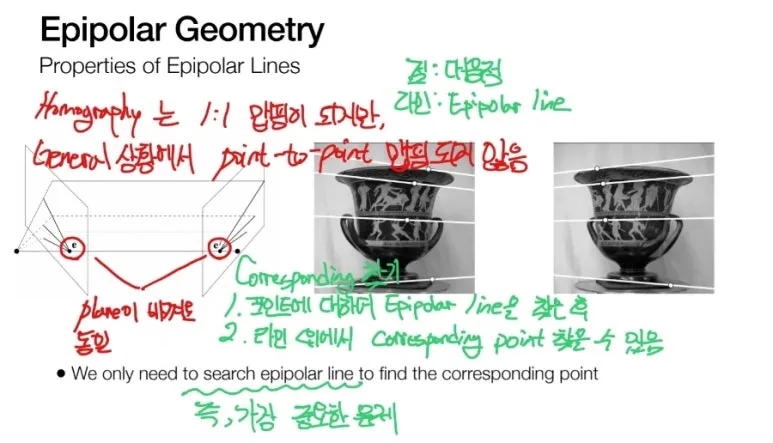
이전에 살펴본 Homograhy 는
두 이미지가 동일한 평면을 촬영한
Plnae to plane 맵핑이기 때문에
1:1 맵핑이 가능하지만,
일반적인 경우,
Depth 를 알지 못하므로,
Point to point 맵핑이 불가능 합니다.
따라서,
대응점을 찾기 위해
Epipolar line 을
먼저 찾게 됩니다.
Epipolar Line을 계산하기 위한 Fundamental Matrix
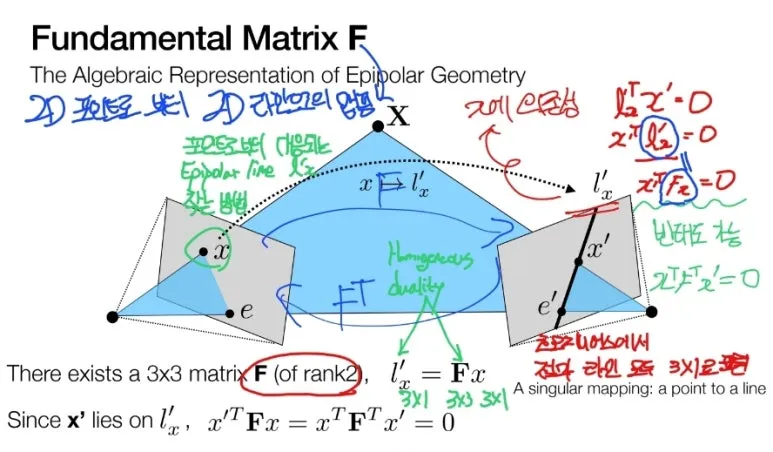
한 쪽의 이미지에 2D point x 를
다른 이미지의 Epipolar line 으로
변환하는 Matrix 를
Fundamental Matrix 라고 합니다.
| 구성 요소 | 설명 |
|---|---|
| Epipole | 상대 카메라 중심이 이미지에 나타난 점 |
| Epipolar Line | 한 이미지의 점이 다른 이미지에서 놓여야 하는 선 |
| Fundamental Matrix | 두 이미지를 연결하는 epipolar 관계의 수학적 표현 |
Fundamental Matrix 는
두 카메라 시점 간의 일반적인
3D 공간에서의 대응점 관계를 가집니다.
Homography 와 차이가 있습니다.
| 항목 | Homography | Fundamental Matrix |
|---|---|---|
| 정의 | 평면 기반 이미지 변환 | 2D 대응점을 3D 공간에서 매핑하는 행렬 |
| 주요 사용 조건 | 동일 평면 촬영 (Plane-to-Plane Mapping) | 임의 3D 장면 촬영 (Two-view Geometry) |
| 대응점 관계 | x ↔ x’ 직접 매핑 가능 | x ↔ x’ 선 위에서 매핑 (Epipolar Line) |
| 자유도 (DoF) | 8 | 7 |
| 선형 제약 조건 | 없음 | Epipolar constraint (x’ᵀFx = 0) |
| 랭크 (Rank) | 일반 행렬 (Rank 3 가능) | Rank 2 (Singular Matrix) |
| 필수 입력 데이터 | 4쌍 이상의 대응점 | 7쌍 이상의 대응점 |
| 카메라 캘리브레이션 필요 | 필요 없음 | 불필요 (Uncalibrated도 사용 가능) |
| 활용 분야 | 이미지 스티칭, 증강현실 | 스테레오 비전, SLAM, 3D 재구성 |
헷갈리시면 안됩니다.
x 에 F 를 곱해서 line’ 을 만들고
x’ 는 line’ 위에 존재하므로
곱하면 0 이 됩니다.

Fundamental Matrix F 는
변환 후 모든 라인이
동일 Epipole 을 가지게 해야하므로
Rank 2 의 Singular matrix 입니다.

즉, 이 식을 만족해야 x, x’ , X
모두 동일한 Plane 에
존재하게 됩니다.
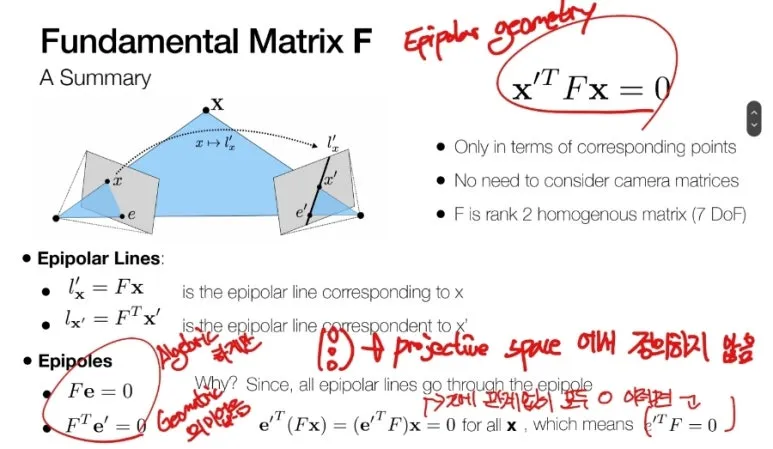
Epipole 에 F 를 곱하면 0 이
나오게 되는데,
Projective space 에서
(0,0,0) 은 정의되지 않습니다.
따라서 Gemetric 의미는 없고
단지, Algebric 하게만
이해하시면 됩니다.
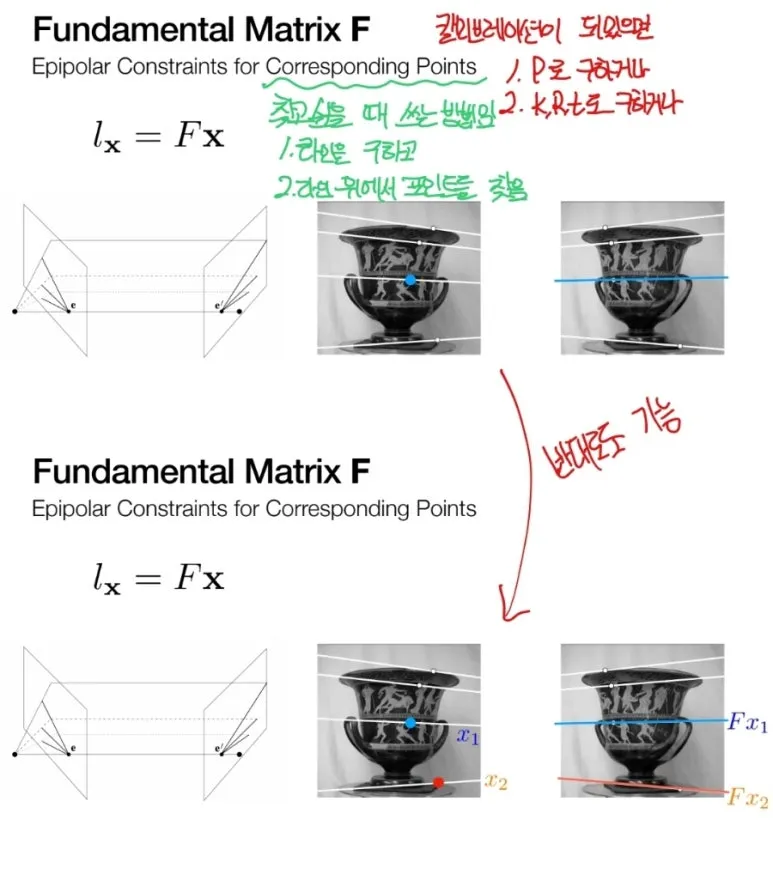
Calibration 없이 대응점을 찾기 위해,
Epipolar Line 을 먼저 구한 뒤,
Line 위에서 대응되는 점을 찾는데
Fundamental Matrix 가 사용됩니다.
| 특징 요약 | 설명 |
|---|---|
| ✅ 랭크 2의 3×3 행렬 | F는 특이값 중 하나가 0인 비가역 행렬이며, Epipolar 제약을 만족하는 구조적 성질을 가짐 |
| ✅ 내부 파라미터(K) 없이 계산 가능 | F는 카메라의 초점거리, 주점 등 내부 파라미터 없이, 오직 외부 위치 관계와 대응점 정보만으로 정의됨 |
| ✅ 카메라 간 상대 위치(R, t)와 대응점쌍으로 계산 | 두 카메라 간의 회전(R), 이동(t), 그리고 이미지에서의 대응점쌍(x, x′) 만 있으면 F 추정 가능 |
Homography 는 주로 평면적인 객체를
촬영한 이미지 간 변환을 다루며,
8 DoF 를 가집니다.
Fundamental Matrix 는
두 카메라가 3D 공간의 장면을
촬영한 경우에 사용되며
7 DoF 를 가집니다.

F 를 표현하는 다양한 방법들에
해당하는 요소를 알고 있다면,
식에 대입하여 구할 수 있고,
아무것도 모른다면,
7 쌍의 대응점을 이용하여
7DoF 를 풀 수 있습니다.
| 항목 | 설명 |
|---|---|
| F | 순수 대응점 기반, 카메라 내부 정보 없음 |
| E (F + Intrinsic parameter) | 내부 파라미터가 반영된 F, 즉 기하적 깊이 의미가 포함됨 |
| R, t | E를 SVD로 분해하면 4가지 해 중 하나로 구할 수 있음 (disambiguation 필요) |
그런 건 난 잘 모르겠고,
Epipolar Geometry는
카메라 사이의 기하 관계이고,
Fundamental Matrix는
한 쪽 점을 다른 쪽 Epipolar Line으로
변환해주는 도구
참고자료
Slide credit : Joo Hanbyul
https://homes.cs.washington.edu/~seitz/talks/3Dhistory.pdf
