DLT란 무엇인가?
이번 글에서는
DLT (Direct Linear Transform)
에 대하여 살펴보겠습니다.
우리는 이전에 투영된 공간에서의
변환에 대해 살펴봤었습니다.
이러한 Homography 변환을 구할 때
DLT 를 사용하게 됩니다.

Input 과 Output 이미지 모두
투영된 공간에서의
2차원 이미지 입니다.
그런데 뭔가 변한 것 같습니다.
이 변환이 무엇인지 찾기 위해서
두 이미지에서 공통인 부분을 찾습니다.
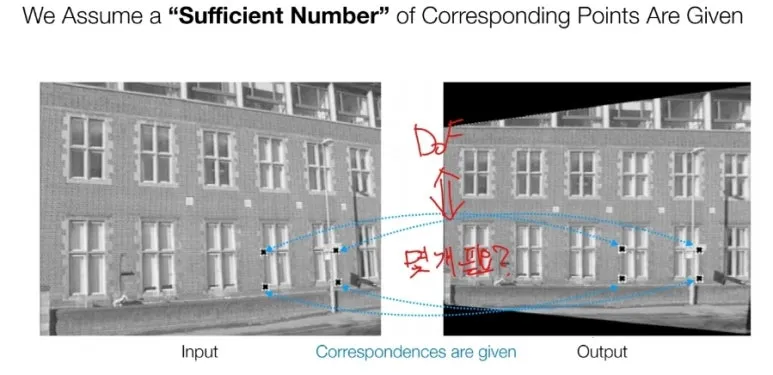
이것을 Correspondence (대응점) 라고 합니다.
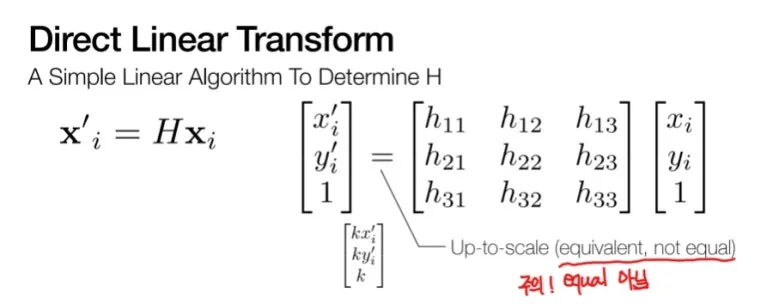
우리는 Homography 가
3×3 행렬인 것을 배웠습니다.
행렬 안에는 9개의 변수가 있지만,
h33 으로 나눠서 총 8개의
변수를 가진 행렬입니다.
오른쪽의 x,y,1 은 Input 이미지의
첫번째 대응점의 좌표이고
왼쪽 x,y,,1 은 output 이미지의
첫번째 대응점의 좌표입니다.
즉, 변환을 통해 식이 성립함을
이용해서 Homography 를 구할 수 있습니다.
대응점(Correspondence)의 의미와 필요성

우리가 방정식을 풀 때,
구하고자 하는 변수의 개수는
몇 개의 식을 가지고 있는지와
연관이 있었습니다.
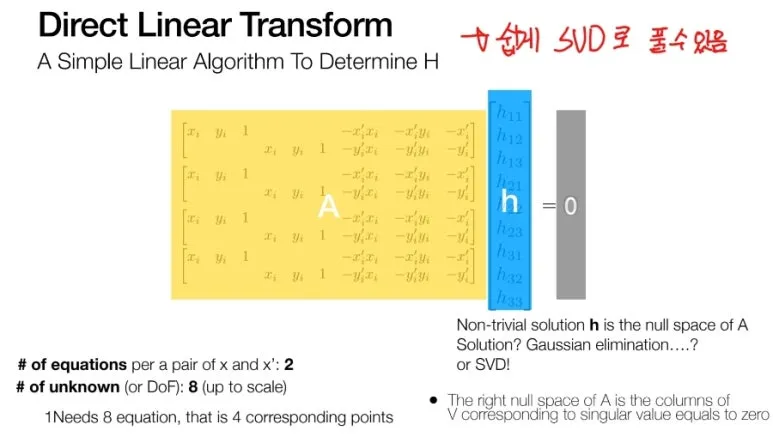
8개의 변수를 모두 구하기 위해서는
총 4쌍의 대응점이 필요하게 됩니다.
이렇게 방정식을 이용하여 풀 수도 있고
SVD 를 이용하여 풀 수도 있습니다.

많을수록 Robust 하다는 것은
다른 수많은 대응점에 대해서도 어느 정도
식이 성립한다는 것을 의미합니다.
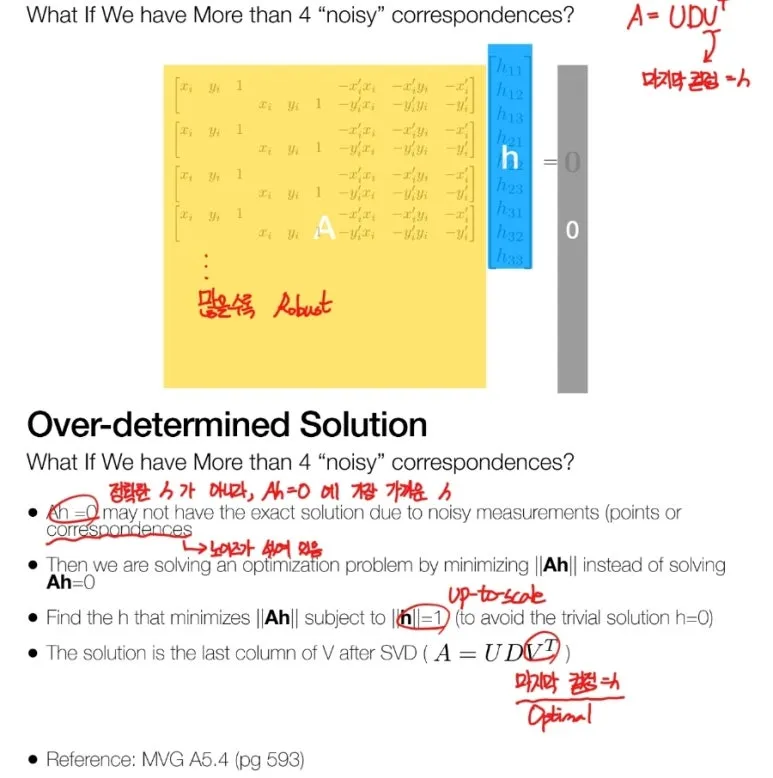
대응점을 이용해서 식을 풀지만,
우리가 실제 세상을 촬영하여
투영된 세상에 가져오는
과정은 매우 복잡합니다.
빛이 공기를 지나서,
물체에 반사되어,
카메라로 들어와서,
렌즈로 굴절되어 빛이 모이고,
CMOS 센서와 같은 곳에 반응을 일으키고,
고품질의 사진을 위한
카메라 안에서의 정제과정을 거치고 등등
어느 과정에서 어떤 노이즈가 섞여있을지
모르기 때문에 우리는 Ah=0 에 근사하는 답을 찾게 됩니다.
그런 건 난 잘 모르겠고,
DLT 는 투영된 공간에서의
평면 변환을 구하기 위해
대응점 이용하여
방정식을 푸는 방법
참고자료
Slide credit : Joo Hanbyul
https://homes.cs.washington.edu/~seitz/talks/3Dhistory.pdf
