이산 확률 변수란 무엇인가?
이번 글에서는
Discrete Random Variable (이산확률변수) 와
Probability Mass Function (확률질량함수) 를
같이 살펴보겠습니다.
이전까지 우리는
Continuous (연속)
Random Variable (확률변수)
Continuous Random Variable (연속확률변수)
Probability Density Function (확률밀도함수)
모두 살펴봤었습니다.
제가 왜 확률과 통계에서
용어의 확실한 이해가
중요하다고 했는지
슬슬 느껴지실 것 같습니다.
용어 자체도 비슷비슷하고
그 안의 내용의 차이도
곰곰이 생각하지 않으면
놓치기 쉽습니다.
그래서 단어만 듣고도
‘아~ 이거’ 바로 나올 만큼의
단단한 초석을 쌓아야 됩니다.
연속 확률 변수와의 핵심 차이
Discrete Random Variable (이산 랜덤 변수)는
Discrete 한 event 들을 정의합니다.
이산은 연속과 달리
특정 event 들로 딱딱 끊어집니다.


예를 들면,
동전을 던졌을 때,
앞면, 뒷면 이런 식입니다.
하지만 우리는 이전에
쥐의 몸무게를 연속으로 살펴봤으므로,
똑같이 쥐의 몸무게를
이산적으로 살펴보겠습니다.
쥐의 무게가 정확히
양의 정수로 떨어집니다.
왜 이번에는 다르냐고요?
그냥 우리가 이렇게 정의 한 겁니다.
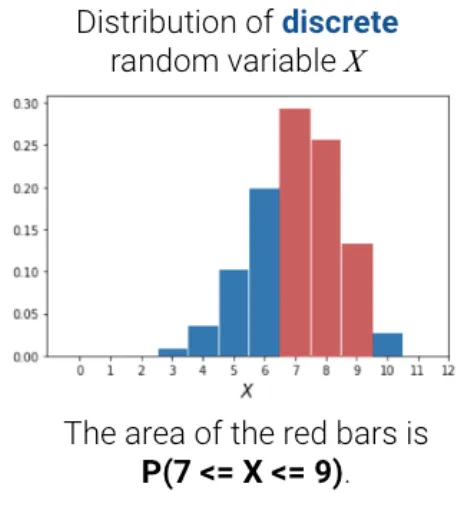
자, x축을 먼저 보겠습니다.
x축은 쥐의 무게입니다.
평균이 7 정도 되는
쥐들의 모임이겠군요
이산적이라고 했습니다.
그 말인즉슨,
8.0000001,
8.0000002,
8.00000564,
이런 값들은 없는 겁니다.
그냥 7,8,9 이런 식입니다.
그런 건 난 잘 모르겠고,
Discrete Random Variable (이산 랜덤 변수)는
구간 Event 가 아니라,
특정 Event 를 의미한다.
PMF는 특정 값의 확률을 직접 계산
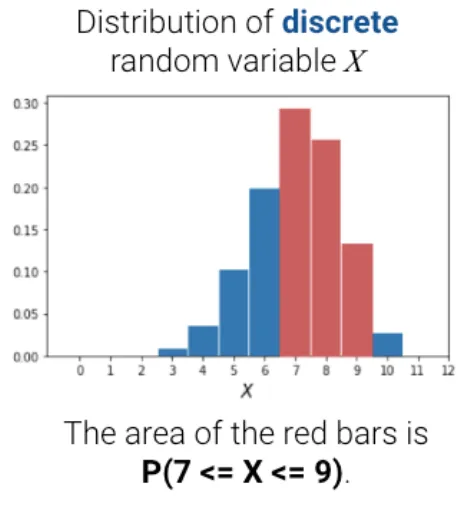
이산 랜덤 변수에서는
P(X=6) = 0.28,
P(X=7) = 0.26,
P(X=8) = 0.13
이런 식으로 이산 랜덤 변수의 값으로
그래프의 y 값 (확률)을
직접 구할 수 있습니다.
우리가 확률을 살펴볼 때,
확률은 0~1 사이의 값이라고 했었습니다.
그러면?
전체 범위의 면적 값을
Sigma (합)으로
다 더하면 1이 되겠네요.
그런 건 난 잘 모르겠고,
Probability Mass Function (확률 질량 함수)는
이산 확률 변수가 이루는 분포이자
특정 값이 확률을 의미
참고자료
https://ds100.org/course-notes/probability_1/probability_1.html

