연속 확률 변수란?
이번 글에서는
Continuous Random Variable (연속확률변수) +
Probability Density Function (확률밀도함수)
에 대해 알아보겠습니다.
매우 밀접한 관련이 있기
때문에 같이 살펴보겠습니다.
사실, 우리는 이미
Continuous (연속) 와
Random Variable (확률변수) 모
두 살펴봤었습니다.
이 두 용어를 이해하시고
‘음~ Continuous Random Variable 은
대충 ~~ 느낌이겠군’
이 되시면 정말 훌륭하신 겁니다.
저는 전혀 안되거든요.
예시를 보도록 하겠습니다.
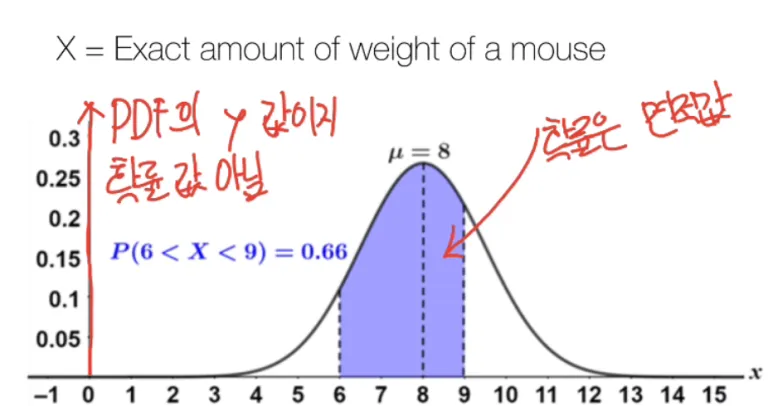
여기서 X는 = 쥐의 무게가 x
값인 경우의 수 입니다.
자, x축을 먼저 보겠습니다.
x축은 쥐의 무게입니다.
평균이 8 정도 되는
쥐들의 모임이겠군요.
그런데,
쥐의 무게가 x=8 일 경우의 수가 있을까요?
연속적이라고 했습니다.
그 말인즉슨,
8,000001 일수도
8.0000002 일수도
8.00000564 일수도 있습니다.
즉, 연속에서 정확히 8일
확률은 0에 수렴합니다.
그런 건 난 잘 모르겠고,
Continuous Random Variable (연속 확률 변수) 는
특정 Event 가 아니라,
구간 Event 를 의미한다.
확률 밀도 함수란?
우리가 확률 변수로
특정 사건을 정의하는 이유는
결국 확률을 구하기 위해서입니다.
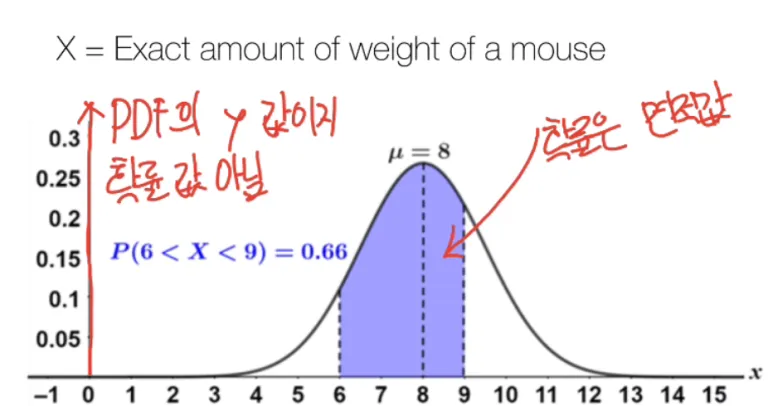
그래프의 y축을 확률이라고
보시면 안됩니다.
이 그래프의 y 축은 PDF 의 y 값입니다.
그래프의 면적이 확률입니다.
Continuous Random Variable (연속 확률 변수)
를 사용하는 그래프를
Probability density function (확률밀도함수)
라고 합니다.
위 그래프에서 구간 [6~9] 확률은
면적 값 0.66 이 됩니다.
의미는 쥐의 무게가 6~9 사이일
확률을 의미합니다.
우리가 확률을 살펴볼 때,
확률은 0~1 사이의
값이라고 했었습니다.
그러면?
전체 범위의 면적 값을
Integral (적분)으로 구하면
1이 되겠네요.
그런 건 난 잘 모르겠고,
Probability density function (PDF) 확률 밀도 함수는
연속 확률 변수가 이루는 분포이자,
면적은 확률을 의미
참고자료
https://www.cuemath.com/data/continuous-random-variable

