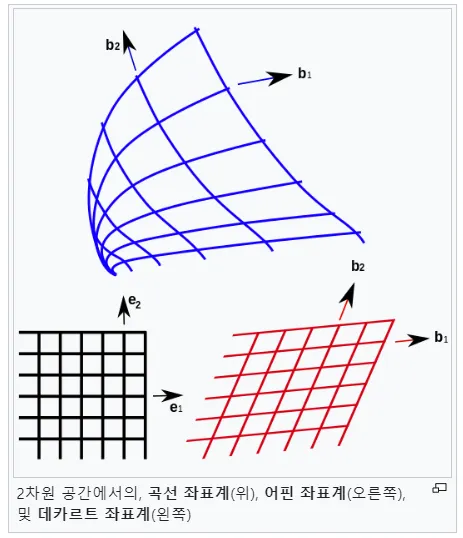
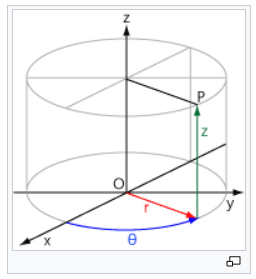
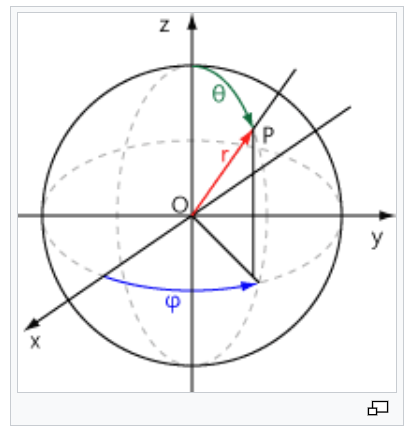
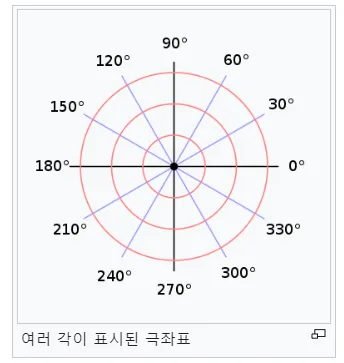
직교 좌표계란? 데카르트, 극, 원통, 구면 좌표계의 관계 이해하기
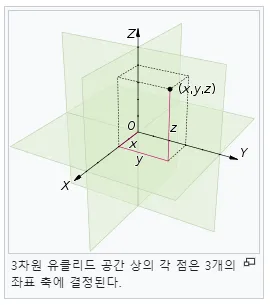
직교 좌표계란 무엇인가? 이번 글에서는 직교좌표계에 대하여 알아보겠습니다. 우리는 데카르트 좌표계, 극 좌표계, 원통 좌표계, 구면 좌표계에 대하여 모두 한 번씩 살펴봤습니다. 이 좌표계들의 공통점은 모두 단위벡터 (basis) 끼리 항상 서로 수직 한 좌표계라는 점입니다. 네. 선형대수학의 기저 맞습니다.정리를 한번 해보겠습니다. 좌표계들 사이의 공통점: 직교성 유클리드 공간이 있습니다. 그 … 더 읽기