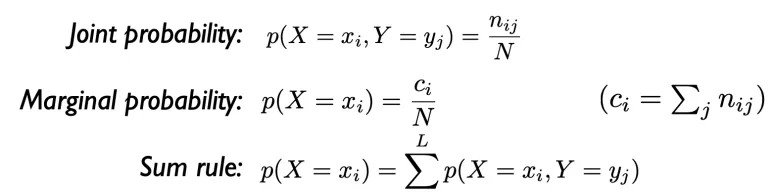선형대 수학과 확률과 통계에 대하여 정리한 카테고리입니다.
Sum Rule이란? 이번 글에서는 Sum rule (합의 법칙)에 대해서 살펴보겠습니다. 우리는 이전에 Joint probability 와 Marginal probability를 살펴봤습니다. Joint probability는 동시에 일어날 확률입니다. 행렬 예시에서는 특정한 행과 열을 가지는 칸을 선택할 확률입니다. Marginal probability는 다른 확률 변수는 무시하는 확률입니다. 행렬 예시에서는 특정한 열을 가지는 칸을 선택할 확률입니다. 행은 신경 쓰지 않습니다. … Read more
Product Rule이란 무엇인가? 이번 글에서는 Product rule (곱 규칙)에 대하여 살펴보겠습니다. 식을 먼저 보겠습니다. xi를 뽑는 Marginal probability에 xi를 뽑은 뒤 yi를 뽑는 Conditional probability를 곱하고 있습니다. 이 2가지의 확률이 동시에 발생할 확률 (Joint probability)는 Conditional probability x Marginal probability두 확률의 곱하고 동일합니다. 이것이 Product rule (곱 규칙)입니다. 여기서 조건부 확률은 이렇게 … Read more
Conditional Probability(조건부 확률)이란? 이번 글에서는 Conditional probability (조건부 확률) 에 대하여 살펴보겠습니다. Conditional probability는 이미 발생한 어느 event 에서 다른 event 가 일어날 확률 입니다. 설명이 어려운데 예시를 살펴보겠습니다. 열을 선택하는 Event가 이미 일어난 뒤 행을 선택하는 Event 가 일어날 확률입니다. 따라서 하나의 열이 선택됬을 때가능한 경우의 수는 ci = 3 입니다. … Read more
Marginal Probability(주변 확률)이란? 이번 글에서는 Marginal probability (주변 확률) 에 대하여 살펴보겠습니다. Marginal probability는 다른 event의 결과에 상관없이 하나의 event 결과만 만족하는 확률입니다. 하나의 Random Variable만 고려한다는 의미 설명이 어려운데 예시를 살펴보겠습니다. 보시면 오로지 열을 선택하는 Event의 결과만 만족하면 됩니다. Random variable X는 열(Column)의 값입니다. 즉 행(row)의 값은 저희의 고려 대상이 … Read more
결합 확률(Joint Probability)이란? 이번 글에서는 Joint probability (결합 확률) 에 대해 알아보겠습니다. 두 개의 Random variable이 동시에 만족하는 확률을 의미합니다. 우리는 Random variable 은 어떠한 event 를 그냥 정의한 것 이라고 했습니다. event 가 2개가 있고 동시에 만족하면 Joint probability 입니다. Joint Probability의 예시 예시를 보겠습니다. 그림과 같이 Matrix (행렬)이 있습니다. 어떤 … Read more
이산 확률 변수란 무엇인가? 이번 글에서는 Discrete Random Variable (이산확률변수) 와 Probability Mass Function (확률질량함수) 를 같이 살펴보겠습니다. 이전까지 우리는 Continuous (연속) Random Variable (확률변수) Continuous Random Variable (연속확률변수) Probability Density Function (확률밀도함수) 모두 살펴봤었습니다. 제가 왜 확률과 통계에서 용어의 확실한 이해가 중요하다고 했는지 슬슬 느껴지실 것 같습니다. 용어 자체도 비슷비슷하고 그 안의 … Read more
연속 확률 변수란? 이번 글에서는 Continuous Random Variable (연속확률변수) + Probability Density Function (확률밀도함수) 에 대해 알아보겠습니다. 매우 밀접한 관련이 있기 때문에 같이 살펴보겠습니다. 사실, 우리는 이미 Continuous (연속) 와 Random Variable (확률변수) 모두 살펴봤었습니다. 이 두 용어를 이해하시고 ‘음~ Continuous Random Variable 은 대충 ~~ 느낌이겠군’ 이 되시면 정말 훌륭하신 겁니다. … Read more
확률 변수란 무엇인가? 이번 글에서는 Random variable (확률 변수) 에 대하여 살펴보겠습니다. ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ 어이가 없습니다. 무슨 말인지 전혀 모르겠습니다. 예시: 동전 던지기와 확률 변수 바로 예시를 살펴보겠습니다. 동전을 던지겠습니다. (앞면, 뒷면)2가지의 events 가 있습니다. 이걸 확률로 나타내기 위해서는 P(동전이 앞면으로 낙하) = 1/2 P(동전이 뒷면으로 낙하) = 1/2 이런 식으로 … Read more
확률의 정의: P(A) = 사건 A가 일어날 확률 이번 글에서는 정말 중요한 확률에 대해 알아보겠습니다. 우리는 Sample space 와 Event에 대한 튼튼한 개념이 있습니다. Sample space(전체 경우의 수)와 내가 정의한 Event(사건)를 만족하는 수를 알 수 있다면 P(A) = Event 가 일어날 확률을 구할 수 있습니다. P() = 확률 A = 내가 정의한 Event … Read more
Event란 무엇인가? 이번 글에서는 Event에 대하여 알아보겠습니다. 복잡합니다. 예시로 의미를 파악해 보겠습니다. Event는 내가 정의한 조건의 결과 집합 우리는 주사위의 Sample space를 살펴봤었습니다. S={1,2,3,4,5,6} 입니다. Event 가 주사위를 던져서 나올 수 있는 수 라고 정의된다면 1도 Event 2도 Event 3도 Event 4도 Event 5도 Event 6도 Event입니다. Event 가 주사위를 던져서 … Read more
