Affine Camera와 일반 카메라의 차이
이번 글에서는
Affine Camera
에 대하여 살펴보겠습니다.

우리가 기본값으로 말하는 Camera 는
Camera center 가 finite 한 위치에 있습니다.
유한한 공간에 있다는 뜻은
해당 위치에서 물체를 볼 때,
멀리 있는 건 작아지고,
가까운 것은 커지는 현상이 발생합니다.
우리의 눈이나 카메라로 볼 때,
발생하기 때문에 익숙합니다.
반면,
Affine Camera 는 Camera cetner 가
Infinite 에 위치합니다.
어떻게 무한한 공간에 위치할 수 있냐면
카메라를 들고 점점 뒤로 가면서
물체가 작아지는 것을 복합렌즈의
Focal length 를 확대하여 동일한 크기를 유지하면
Camera center 는 Infinite 에 위치하게 됩니다.
카메라 중심이 무한에 있다는 의미

우리가 Homography 에서 살펴봤듯이
Affine transformation 은
평행을 유지하는 변환이였습니다.
Affine camera 도
평행을 보존한다는 특징이
동일하게 있습니다.

항상 평행 선이 보존되야 하므로,
3D Ideal point 를 projection 시키면
항상 2D ideal point 가 됩니다.
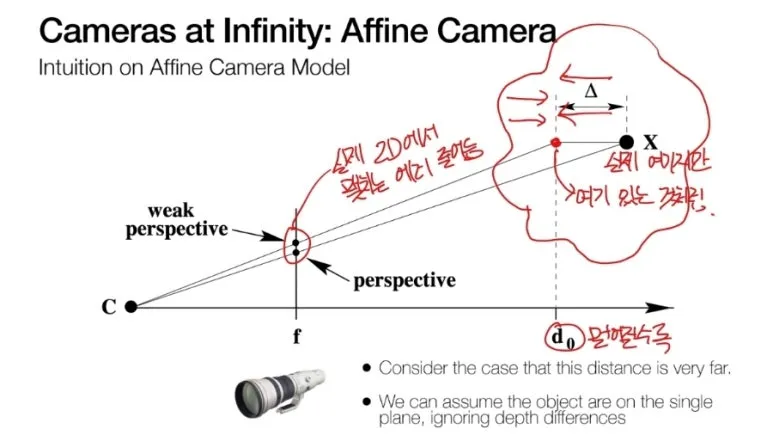
Camera center 가 무한한 위치에 있다는 것은
실제 3D point 의 위치가 달라도
projection 하면 실제 점의 위치가 멀수록
2D 에서의 에러가 줄어들게 됩니다.
직관적인 예를 들어보면,
우리가 북극성을 볼 때,
보고 있는 사람의 위치는 상관없이
항상 동일한 위치에 별이 있다고 느낍니다.
보고 있는 사람의 위치의 차이가
떨어져 있는 거리에 비해
너무나도 작아 무시할 수 있기 때문입니다.
| 항목 | 일반 카메라 (핀홀) | Affine 카메라 |
|---|---|---|
| 카메라 중심 위치 | 유한한 위치 (finite) | 무한대 위치 (infinity) |
| 원근 효과 (Perspective) | 존재 | 없음 (parallel 유지) |
| 평행선 유지 여부 | 수렴 (vanishing point 생성) | 항상 유지 |
| 투영 모델 예시 | Pinhole Projection | Orthographic, Weak Perspective 등 |
| 계산 복잡도 | 비선형 (Non-linear) | 선형 (Linear) |
| 장점 | 실제 원근 표현 가능 | 계산 단순화, 근사 모델로 널리 사용됨 |
Orthographic, Weak Perspective 모델
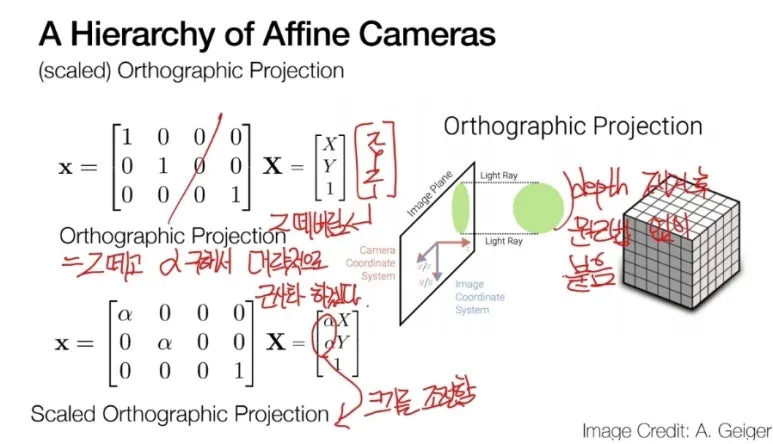
아예 depth 를 지워버리고,
projection 을 진행하는
Orthographic Projection 도 있습니다.
평행을 유지하기 때문에
Affine Camera model 안에 속하게 됩니다.
여기에 단순히 Scaled alpha
값을 추가해서
projection 된 객체의
크기를 조절하기도 합니다.
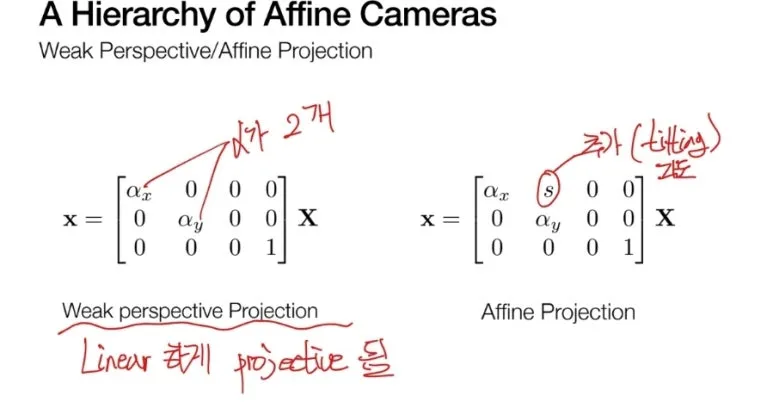
이렇게 Affine camera model 은
평행을 유지한다는 특징을 가지고,
Affine projection,
Weak perspective projection,
Orthographic projection 을 포함합니다.
복잡하게 그냥 카메라 모델을 사용하지 않고,
Affine 카메라 모델을 따로 쓰는거지?
라고 의문이 드실껍니다.
생각보다, Camera center 가
무한한 위치에 있지 않더라도,
상당히 멀리만 있으면 평행을
어느정도 유지하는 projection 이
잘 발생하기 때문에
이를 만족한다고 가정하고
Linear 하게 수식을 풀어 버릴 수
있다는 장점이 있기 때문입니다.!
그런 건 난 잘 모르겠고,
Affine camera 는
Linear (선형적) 이면서
평행을 유지하는 projection
참고자료
Slide credit : Joo Hanbyul
https://homes.cs.washington.edu/~seitz/talks/3Dhistory.pdf
