Homogeneous Coordinates란?
이번 글에서는
Homogeneous coordinates
에 대하여 살펴보겠습니다.
우리는 이전에 유클리드 기하학과
사영 기하학에 대해 살펴봤습니다.
Homogeneous coordinates 는
Projective Geometry 에서
사용하는 좌표 시스템 입니다.
Homogeneous coordinates 에서만
정의되는 여러 성질들이 있습니다.
대표적으로 Euclidean Geometry 에서
사용하는 좌표 시스템에 추가적인 차원을
도입하여 점을 선과
동일하게 정의할 수 있습니다.
(Up-to-scale)
이것이 무엇을 의미하는지 살펴보겠습니다.
왜 Homogeneous Coordinates가 필요한가?
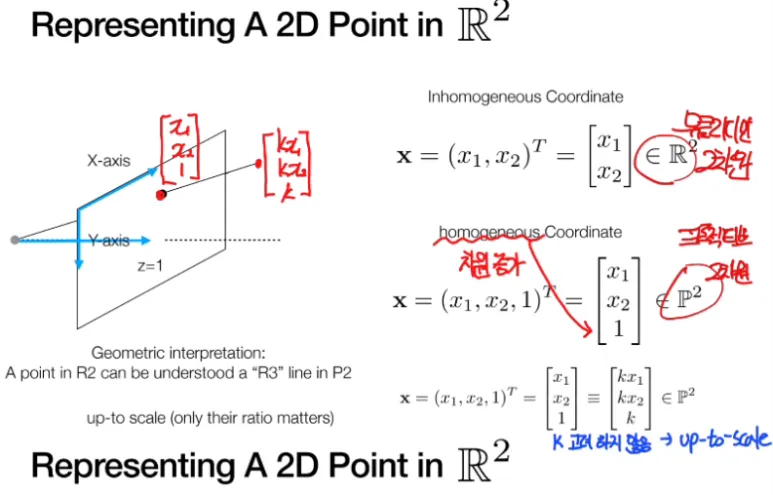
우리가 알고 있는 2차원은 (x,y) 이런 식입니다.
하지만 Homogeneous coordinate 에서는
차원을 하나 추가하여 (x,y,1) 이렇게
정의하고 있습니다.


이렇게 표현하게 되면 추가한 차원이
0 값을 갖는다면 Infinity point 라고
정의할 수 있습니다.
하지만 추가된 차원에 값이 0이 아니라면,
Up-to-scale 이기 때문에 (x,y,1) = (2x,2y,2) 와
동일해지는 성질이 있습니다.
Homogeneous Coordinates 에서의 Duality
직관적이지 않기 때문에,
예시를 한번 보겠습니다.
Projective Geometry 는
카메라를 통해 본 세상이라고 했었습니다.
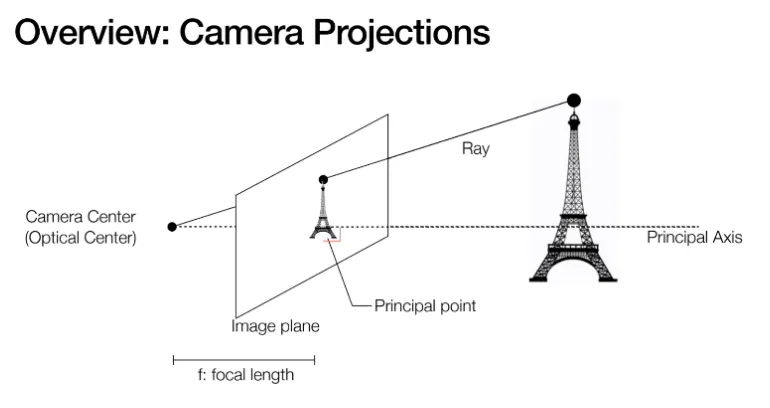
우리가 카메라로 에펠탑을 보고 있습니다.
실제 에펠탑의 꼭대기 위치의
생김새가 우리 카메라로
들어와서 찍히게 됩니다.
Image plane (= camera sensor) 에
에펠탑 꼭대기 모양이 맺힌 위치와
실제 에펠탑 꼭대기 위치는
우리가 알고 있는 세상에서는 다릅니다.
(에펠탑은 저 멀리 있고, 카메라
센서는 내가 들고있는 카메라 안
어딘가에 있으니까요)
하지만 Projective Geometry 에서는
두 점이 동일합니다.
즉, Ray 로 표시된 선분 위에 존재하는
모든 점들을 동일한 표기법으로
정의할 수 있습니다.
Line = Point 사실상 표기법이 같기 때문입니다.
이것을 Duality (이중성) 이라고도 합니다.
Homogeneous coordinate 에서는
다양한 성질들이 있습니다.
정말 기본적인 몇 가지만 살펴보겠습니다.
Homogeneous Coordinates 에서의 특징

Line 과 Point 의 내적 값이
0 을 갖는다는 것은
Point 가 Line 위에 존재함을 뜻합니다.

2 개의 Points 의
외적 값은 Line 입니다.

2개의 Lines 의 외적 값은
교차점 (Point) 입니다.
무한대 점과 평행선의 교차
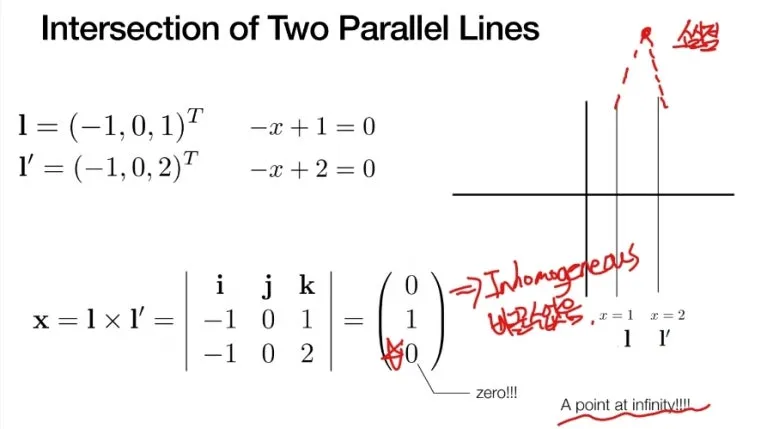
이렇게 정의 된 Homogeneous coordinates 성질들을
이용해서 2개의 평행한 Lines 의
교차점을 구해 보겠습니다.
마지막 차원 값이 0 이 나옵니다.
우리가 처음에 정의했던
Infinity point 가 등장하게 됩니다.
정말 신기하지 않나요??
| 항목 | Euclidean Coordinates | Homogeneous Coordinates |
|---|---|---|
| 좌표 형태 | (x, y), (x, y, z) | (x, y, w), (x, y, z, w) |
| 차원 수 | n | n+1 |
| 무한대 점 표현 | 불가능 | w=0일 때 무한대점 표현 가능 |
| 스케일 불변성 | 없음 | (x, y, w) = (kx, ky, kw) 동일 의미 |
| 평행선 교차 표현 | 불가능 | 무한대점에서 교차 가능 |
| 점 ↔ 직선 관계 | 별도 정의 필요 | 내적/외적으로 상호 변환 가능 |
그런 건 난 잘 모르겠고,
Homogeneous coordinates 는
카메라로 본 세상을
정의하는 좌표계
(Line = Point)
참고자료
Slide credit : Joo Hanbyul
