Sum Rule이란?
이번 글에서는
Sum rule (합의 법칙)
에 대해서 살펴보겠습니다.
우리는 이전에
Joint probability 와
Marginal probability를
살펴봤습니다.
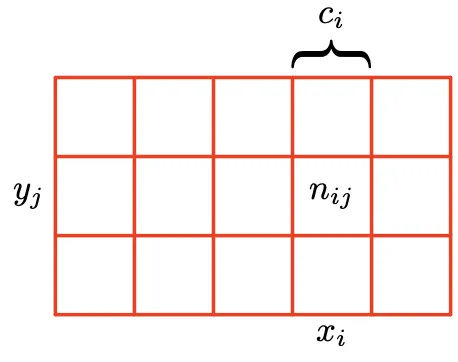
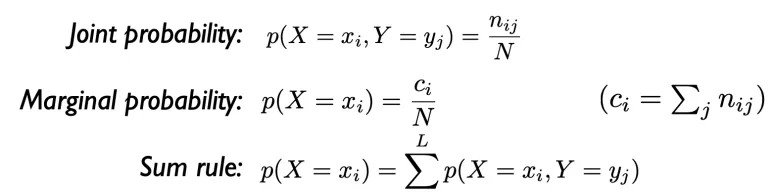
Joint probability는
동시에 일어날 확률입니다.
행렬 예시에서는
특정한 행과 열을 가지는 칸을
선택할 확률입니다.
Marginal probability는
다른 확률 변수는
무시하는 확률입니다.
행렬 예시에서는
특정한 열을 가지는 칸을
선택할 확률입니다.
행은 신경 쓰지 않습니다.
(정의하기에 따라 다름)
Sum rule 을 이용하면
여러 Joint probability 더해서
Marginal probabilirty 을
만들 수 있습니다.
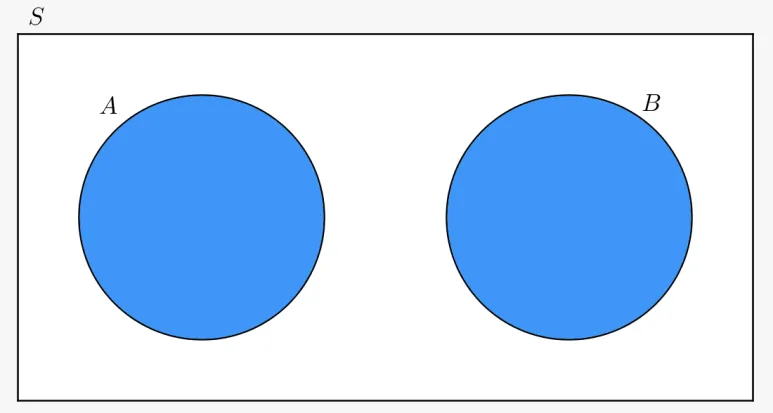
단, Event 들이
상호 배제적인 특성을
가져야 합니다.
서로의 확률에 영향을
끼칠만한 겹치는
부분이 없는 거죠.
Sum Rule의 전제: 상호 배제적인 사건
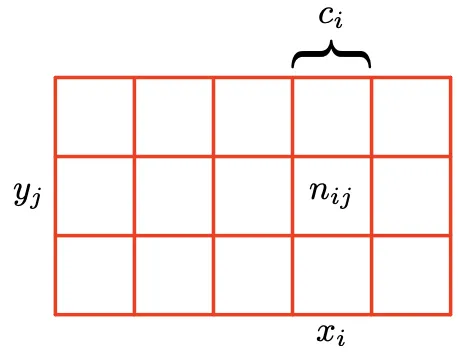
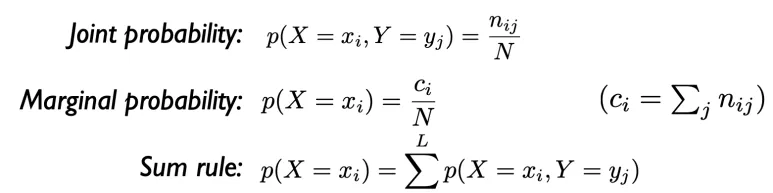
Marginal probability
4번째 열을 선택할
Marginal probability
값은 3/15입니다.
Joint probability
4번째 열 + 1번째 행을 선택할
Joint probability
값은 1/15입니다.
4번째 열 + 2번째 행을
선택할 Joint probability
값은 1/15입니다.
4번째 열 + 2번째 행을
선택할 Joint probability
값은 1/15입니다.
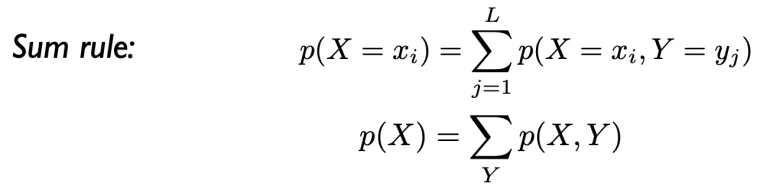
Sum Rule을 활용한 확률 계산 예시
Product rule 에서 예시 문제를 봤었습니다.
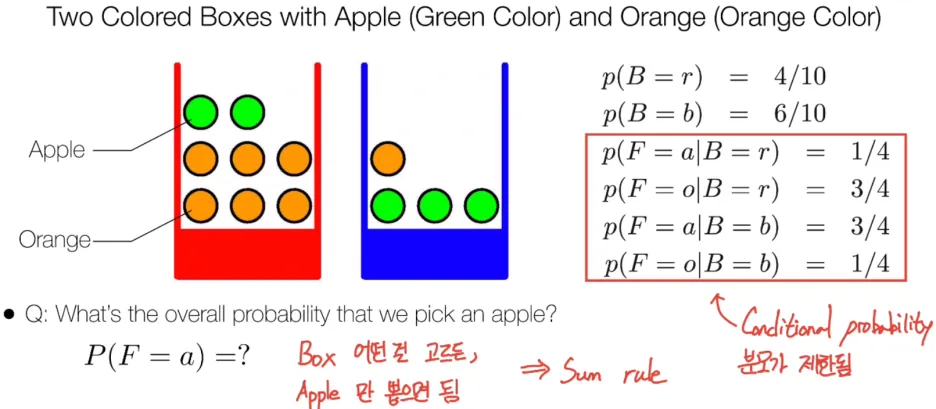
Product rule 로 구한 p(F=a) 확률과
Sum rule 을 이용하면
p(F=o) 확률을
구할 수 있습니다.
그런 건 난 잘 모르겠고,
Sum rule 은
상호 배제적인
Joint probability 확률을 모두 더해서
Marginal probability 확률을 구하는 것
