선형 변환이란 무엇인가?
이전 글에서 살펴본 선형 변환을
어떻게 수치적으로 기술할까요?

일단 Input vecor 와
Output vector 를
표기할 수 있어야 합니다.
기저(Basis)와 벡터 표현
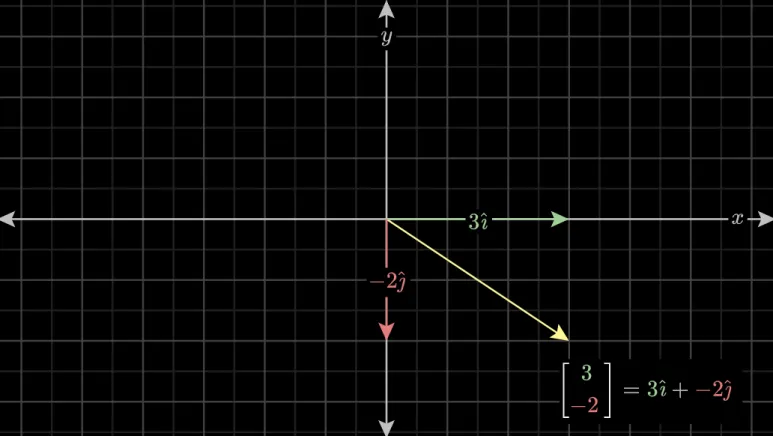
2차원 공간 위에서 벡터를 표현하기
위해 두 기저벡터를 사용하겠습니다.
[-1,2] 라는 벡터를 기저 벡터로 표현한 뒤
Linear Transformation (선형 변환) 해보겠습니다.
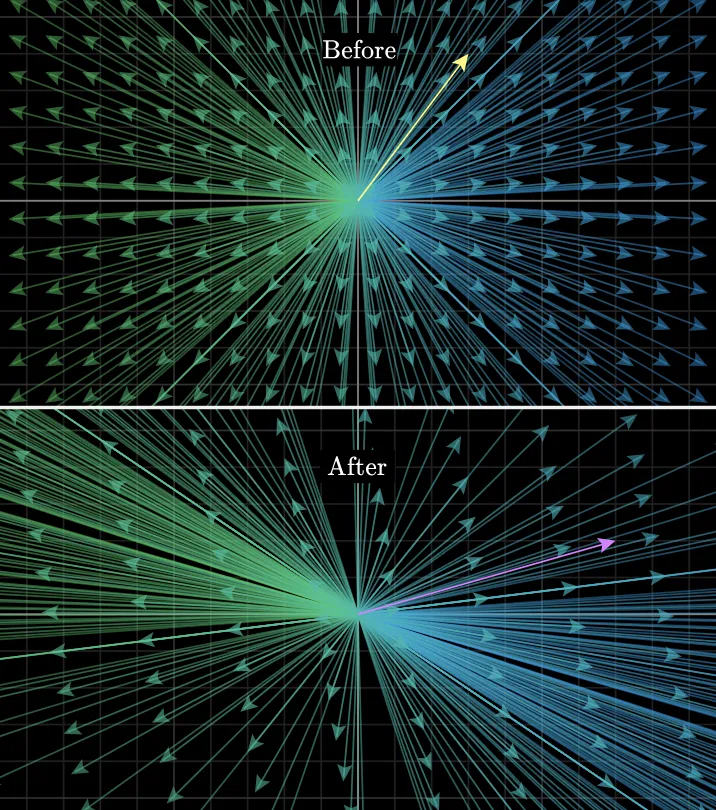
선형 변환과 격자선의 관계
선형 변환은 평행하고 균등하게
격자선을 움직였었습니다.

이렇게 변환된 격자선 위에서도
기존의 선형결합 방식이
그대로 유지됩니다.

변환된 i hat 과 변환된 j hat 를 알고 있으므로,
단순히 계산하여 변환된 벡터를 구할 수 있습니다.
행렬은 선형 변환을 표현하는 방법

즉, i hat 과 j hat 이 어떻게
변환되는지를 알고있으면
벡터가 어떻게 선형변환 되는지
수식적으로 구할 수 있는 것이죠.

i hat 이 어떻게 변하는지,
j hat 이 어떻게 변하는지를
2×2 matrix(행렬)
로 표현할 수 있습니다.

2×2 행렬이 있다면 어떠한 벡터라도
2차원 선형 변환 후 어디로
움직이는지 계산 할 수 있습니다.
정리하자면,
행렬은 선형변환을
설명하는 정보를 묶어
표현하는 방법인 것이죠.

1열은 첫 번째 기저벡터가 도달하는 곳
2열은 두 번째 기저벡터가 도달하는 곳으로 말이죠.

우리는 행렬의 곱하는 방법을 그냥 외웁니다.
이런 의미가 있는지 전혀
고려하지 않고 공부를 하고 있습니다.

[-2,-3] 벡터가 주어진 행렬로 기저 벡터가
어떻게 변환을 가지고 최종적으로
선형 결합을 통하여
어떠한 위치에 도착하는지 이해하면
재미를 느끼는 사람이
조금이라도
더 생길텐데 말이죠.
예시: 회전 변환 행렬과 공간 변형
예시를 좀 살펴보겠습니다.

회전 변환 행렬은 위와 같습니다.
i hat 의 기저벡터는 변환이
없는 선형변환 입니다.


두 기저벡터가 선형종속 관계이면
선형 변환은 전체 2차원 공간을 직선으로
찌그러트려 차원이 축소됩니다.
우리는 앞으로 행렬을 볼 때마다
일종의 공간 변환으로
해석할 수 있습니다.

