Transformation(변환)이란 무엇인가?
Transformation (변환) 은
함수의 다른 말로,
입력값이 들어가면 출력을
내놓는 구조입니다.
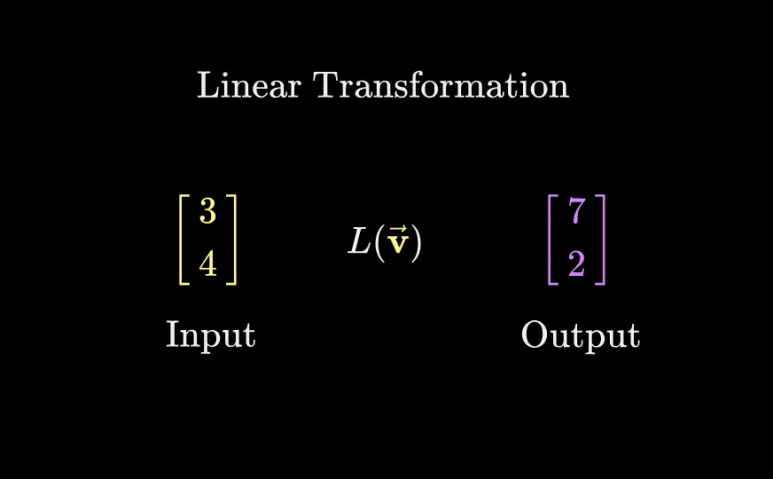
선형대수학에서의 변환은
입력값과 출력값이
벡터입니다.
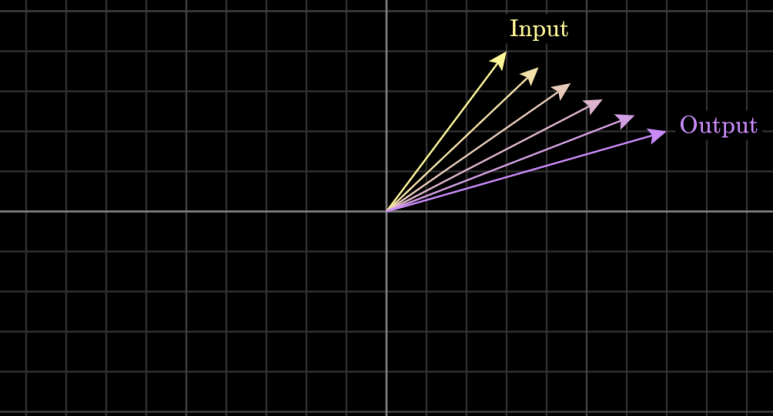
굳이, 함수라는 용어를 사용하지 않고
변환이라고 표현하는 이유는
움직임을 내재하고
있기 때문입니다.

어느 공간에 있는 모든 벡터를
동일한 규칙의 변환을 통해
이동시킬 수 있습니다.
공간 변형으로 바라본 선형 변환
이전 글에서 다뤘던 내용처럼
화살표를 점으로
표현해보겠습니다.
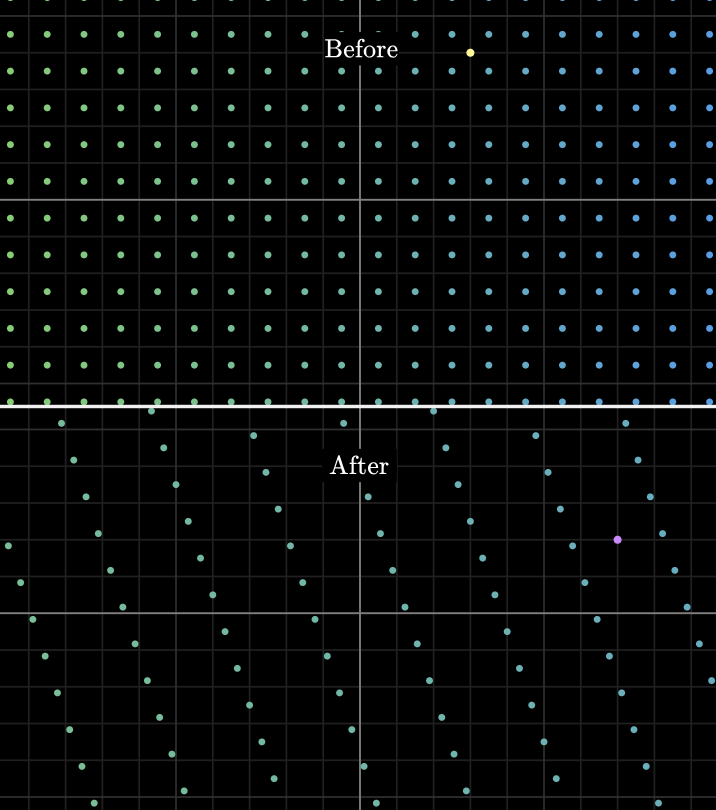
2차원 공간위에 정의된
모든 점들이 다른 곳으로
이동하고 있습니다.
즉, 이것은 공간 자체의
변형이라고
볼 수 있습니다.
원래의 공간을 정의하는 격자를
남겨둔 상태로 변환을
적용 시켜 보면 직관적으로
공간의 변형이 이해됩니다.
Linear Transformation(선형 변환)의 두 가지 조건

다시 돌아와서,
Linear Transformation (선형 변환) 을 살펴보면
1.직선은 직선으로 변형
2.원점은 고정 유지
2가지 특성을 만족하는
변환으로 제한됩니다.
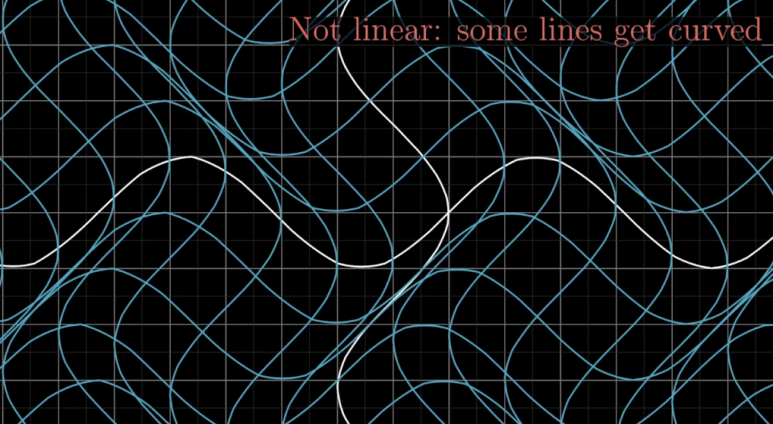
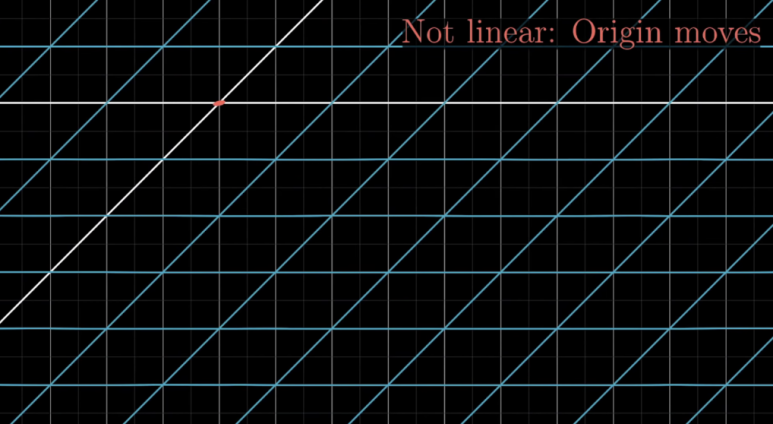
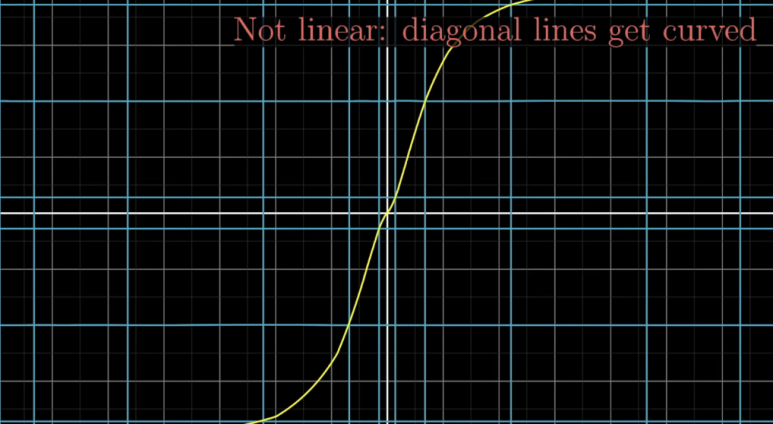
이러한 변환은 선형 변환이 아니게 됩니다.

격자선은 반드시 평행하고
균등한 상태를
유지해야 합니다.
