벡터의 3가지 관점
선형대 수학에서의 가장 기본
구성 요소는 Vector(벡터) 입니다.
그렇다면, 벡터는 무엇일까요?

물리학적 관점
물리학적 관점에서의 벡터는
길이와 방향으로 정의되는
화살표 입니다.
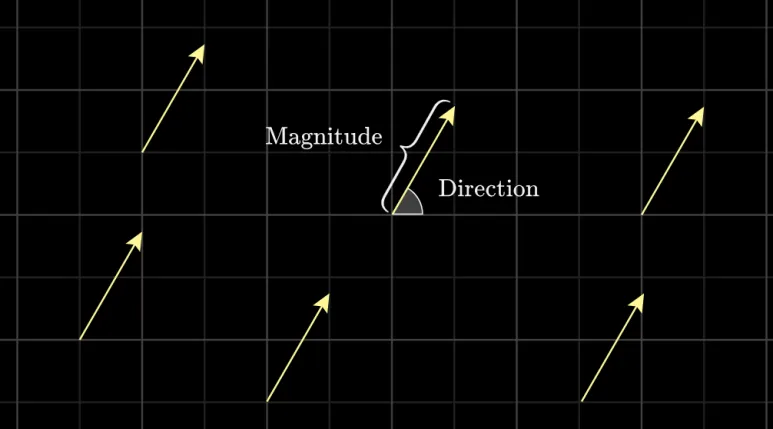
이 공간에서 정의된 벡터들은 모두
길이와 방향이 같으므로
동일한 벡터입니다.
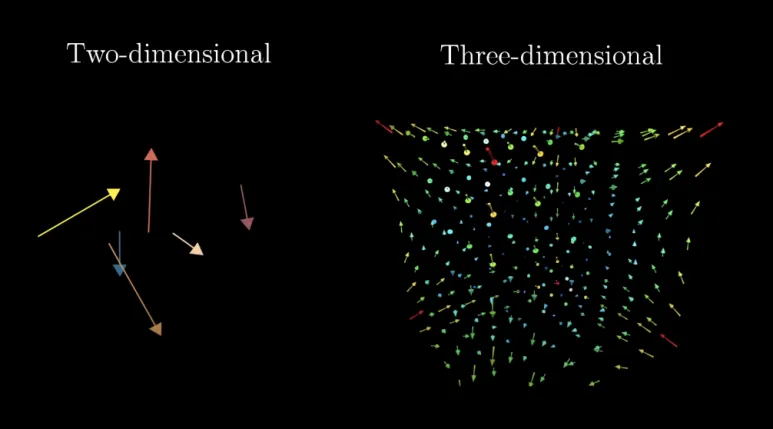
정의되는 공간에 따라
벡터의 차원도 변하게 됩니다.
컴퓨터공학적 관점
컴퓨터공학적 관점에서는 벡터는
정렬되어 있는 숫자 배열입니다.
어떤 집을 사기 위헤 데이터 분석을
한다고 가정했을때,
고려 요소가 집의 크기와 가격 뿐이라면
아래와 같이 나타낼 수 있습니다.
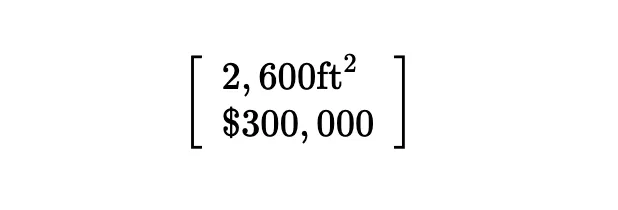
첫 번째 숫자는 집의 크기을
두 번째 숫자는 집의 가격을 의미하므로
정렬된 순서는 바뀌며 안되며,
위 벡터는 2차원 벡터입니다.
여기서 2차원 이라는 말은
단지 숫자가 두 줄로
배열됐음을 의미합니다.
수학적 관점
(동영상에는 일단 스킵하자고 설명하지만, 아래는 저의 주관적 해석입니다.)
수학적 관점에서 벡터는 공간 내의
점들 간의 상대적 위치를
설명하는 도구입니다.
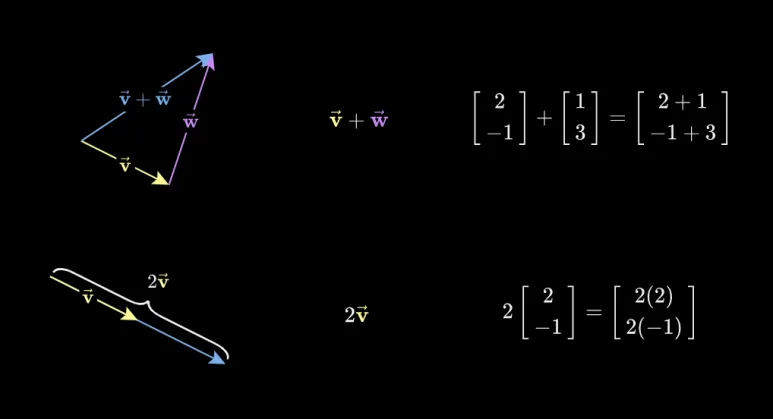
이러한 벡터를 그림과 같이 더하거나
곱하여 공간의 구조를 이해하고
다루는데 응용할 수 있습니다.
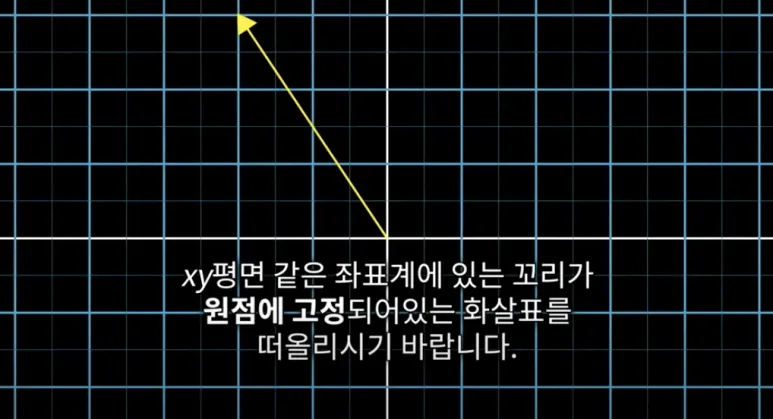
다른 관점에서의 해석과는 살짝 충돌이 있지만,
선형대수학에서 벡터를 떠올리면
아래 그림과 같이 좌표계의 원점에서
시작되는 화살표를 떠올리시기 바랍니다.
갑자기 좌표계에 정의된 화살표를
떠올리라고 하므로,
Coordinate system (좌표계) 에
대하여 살펴보겠습니다.
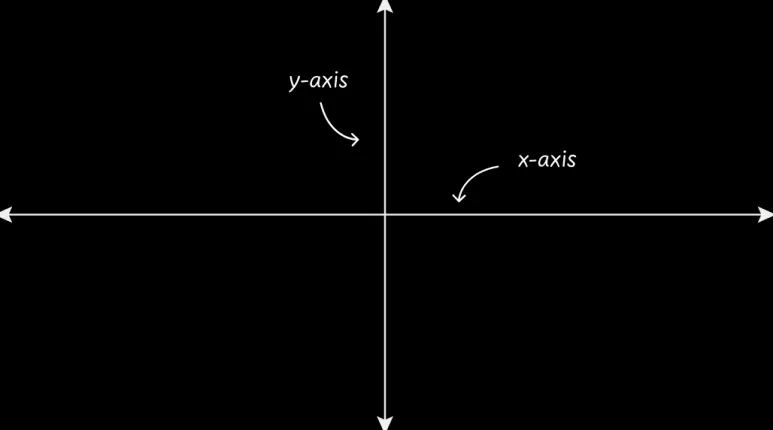
수평선을 정의하는 x 축과
수직선을 정의하는 y 축이 있는
2차원이 있습니다.
x축과 y축이 교차하는 지점이 Origin(원점)이며,
여기서 정의된 공간의 중심이자
모든 벡터의 뿌리입니다.
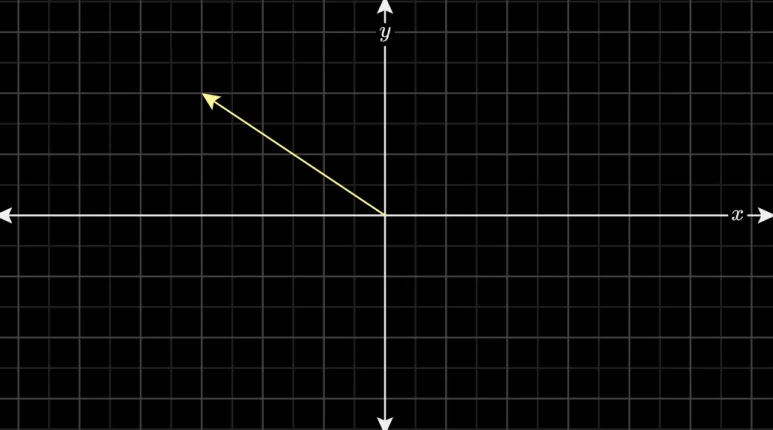
임의의 길이를 나타내는 눈금을 표시하여
격자를 만들면 좌표계가 됩니다.
벡터의 좌표는 원점에서 시작하여 벡터의 끝점까지
도달하는 방법을 설명하는 한 쌍의 숫자로 구성됩니다.
첫 번째 숫자는 x 축을 따라 얼마나 갈지를,
두 번째 숫자는 y 축을 따라 얼마나 갈지를 알려줍니다.
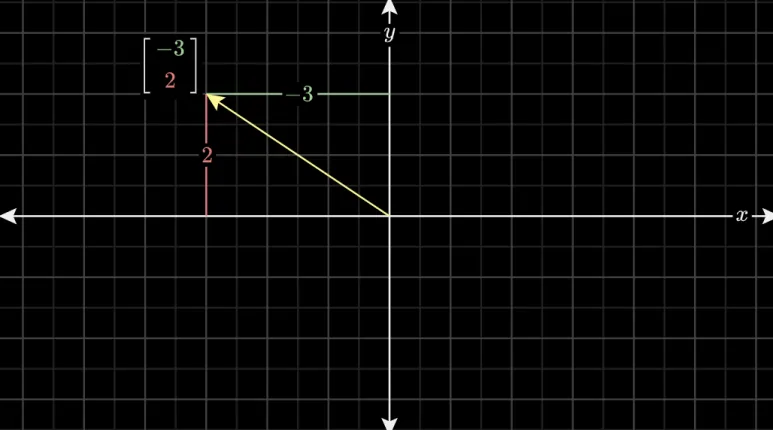
따라서, 위와 같이 벡터를 표현할 수 있습니다.
어라? 그냥 (-3,2) 위치한 점 아닌가?
처럼 질문이 떠오를 수 있습니다.
점과 벡터를 구분하기 위해 관례적으로
숫자 쌍을 대괄호로 묶어 수직으로 씁니다.
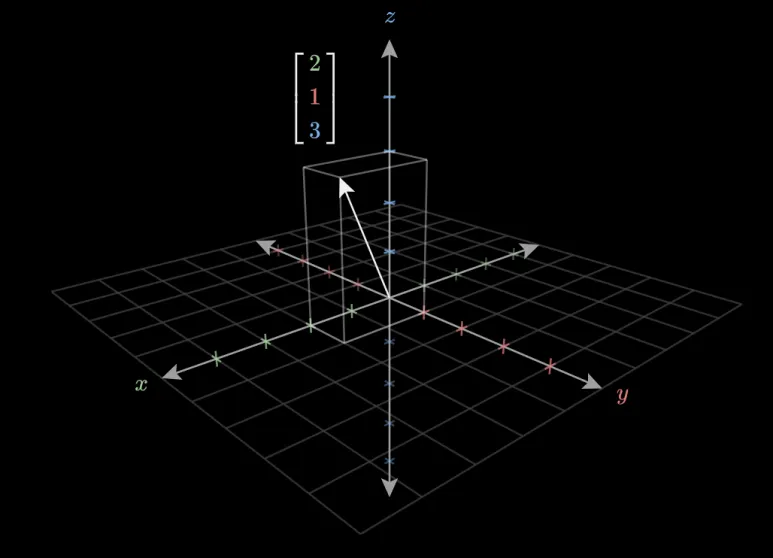
3차원 공간은 3개의 축으로 정의할 수 있으며,
3개의 숫자를 연속으로 나열하여
벡터를 정의할 수 있습니다.
사실, 선형대수학을 어떠한 관점으로
해석하느냐는 중요하지 않습니다.
선형대수학의 용도는 다양한 대상과
그들 사이의 상호작용을
해석하는 능력을 다루는 것입니다.
