2D Angle과 3D Solid Angle의 개념
이번 글에서는
Photometric stereo 에서
자주 사용되는 단위들에
에 대하여 살펴보겠습니다.
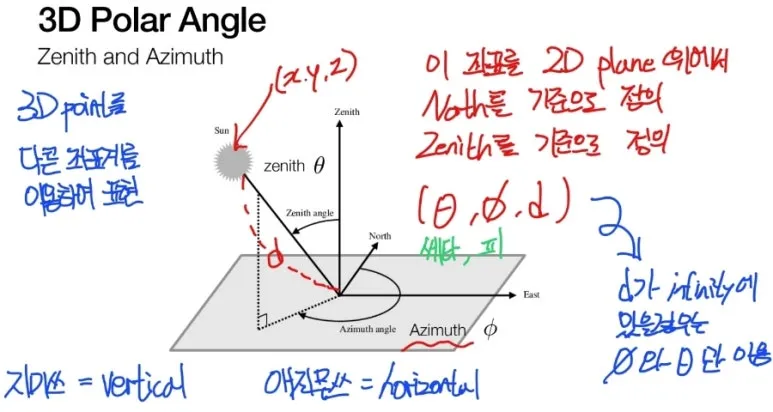
3D Polar Angle 은
3D 위치를 (x,y,z) 로
표현하는 방법 대신에,
2개의 각도와,
1개의 거리로
표현하는 방법입니다.
(쎄타,피,거리)
쎄타는
2D plane 위에서 North를
기준으로 정의되며,
피는
2D plane 과 수직한 방향의
Zenith 를 기준으로 정의됩니다.
거리 d 는
해당 위치까지의 거리입니다.
우리가 이전에 배웠던
Infinity point 에 위치한다면
d는 생략할 수 있습니다.
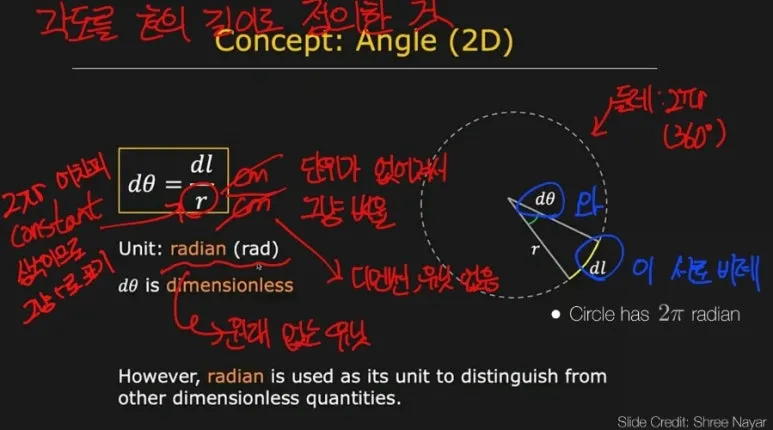
라디안 은
2D 원 에서의 각도를
호의 길이와 반지름의 길이의 비율로
표현한 것을 의미합니다.
원의 전체 둘레가 2x파이 x 반지름 이므로,
각도 쎄타가 주어졌을 때,
원에서 해당되는 호의 길이를 이용하여,
각도를 표현할 수 있습니다.
전체 원의 둘레에서
2x파이 는 상수이므로
단순히 r 로 줄여줄 수 있습니다.
길이의 비율을 이용하는 Radian 은
cm 단위가 소거되기 때문에
Dimension 과 Unit 이
없다는 특징이 있습니다.
여기서 차원(Dimension) 과 Unit(단위) 가
없다는 뜻은 Measurement Unit (측정 단위)
즉,
길이, 면적과 같은 물리적 특성이
없다는 것을 의미합니다.
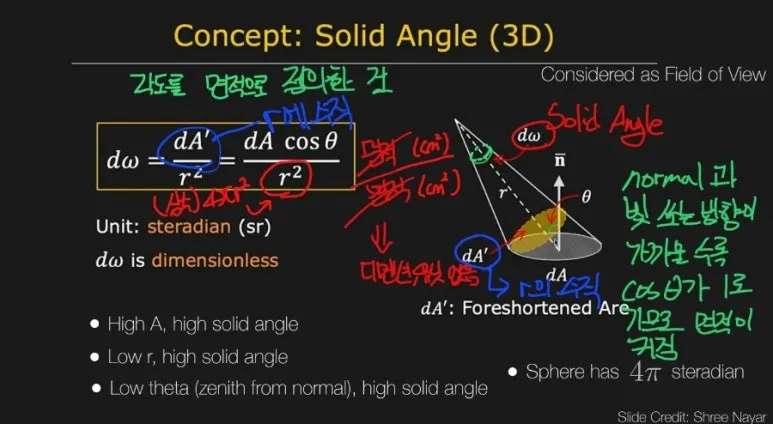
스테라디안 은
3D 원뿔에서의 각도를
구의 전체 면적과
Foreshortened Area 면적의 비율로
표현한 것을 의미합니다.
Foreshortened Area 는
Surface normal 방향과
빛의 방향이 일치하지 않을 때,
면적을 cos 각도만큼
줄여준 것을 의미합니다.
음… 쉽게 말하면
원뿔 모양으로 나가던 빛이
평평한 땅과 만나
그림과 같이
비추는 영역으로
생각할 수 있습니다.
일부 빛이 도착하는 거리가
짧아지기 때문에 타원이 됩니다.
여기서도 4x파이 가 상수이므로,
단순히 r 제곱을 전체 면적으로
사용하고 있습니다.
또한 마찬가지로
면적이 소거되므로,
Unit 이 없습니다.
단위 면적 당 빛의 양
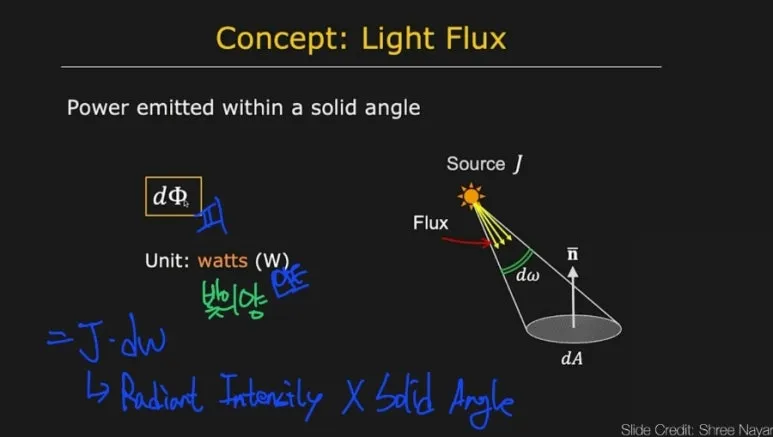
와트 는
Solid angle 안에서
방출되는 빛 입니다.
단위는 와트를 사용합니다.
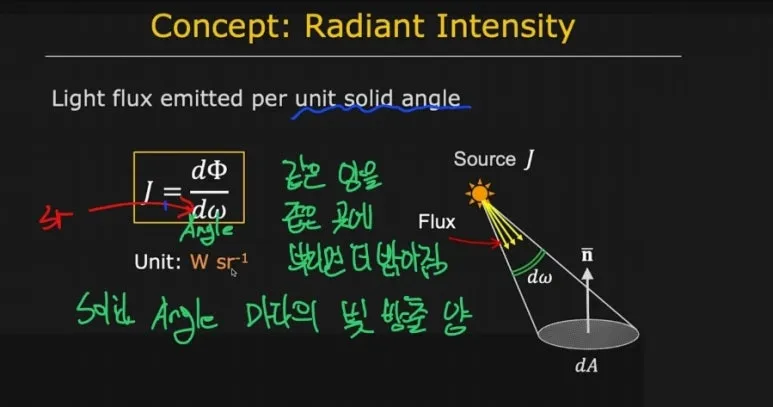
와트 퍼 스테라디안 은
Unit solid angle 마다 방출하는
Light flux 를 의미하고,
J (Radian Intensity) 라고 합니다.
따라서, 방출되는 빛의 양을
Unit solid angle 로
나눠주게 됩니다.
여기서의 Unit 은 단위 표면적
=
즉 , 일정한 면적 단위로
정의된 영역 을 의미합니다.

와트 퍼 제곱미터는
E (Surface Irradiance) 는
Unit surface area 마다
들어오는 빛을 의미하고
E (Surface Irradiance) 라고 합니다.
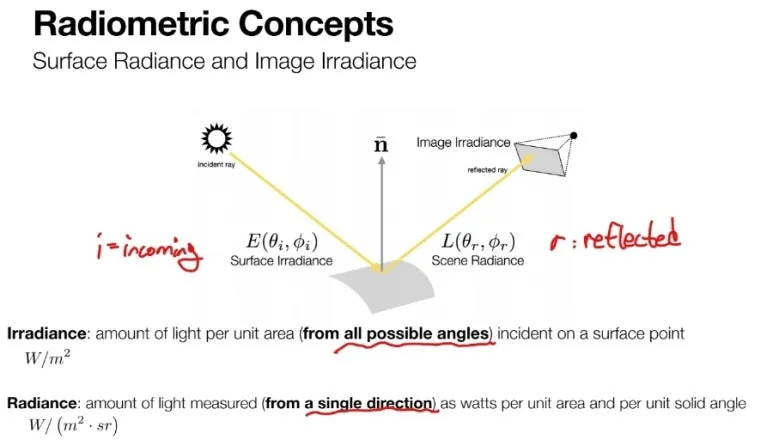
빛은 어느 한 표면에
들어오는 빛
=
Irradiance
그리고
한 표면에 부딪쳐
다른 방향으로 나가는 빛
=
Radiance 로
구분할 수 있습니다.

와트 퍼 제곱미터 퍼 스테라디안 는
E (Surface Irradiance) 를 받은 후
다시 특정 View point 로 반사를 할 때,
측정된 밝기를 의미하고
L (Surface Radiance) 라고 합니다.
즉, 어떠한 각도에서 해당 영역을
봤을 때 가지는 빛의 양
이라고도 해석할 수 있습니다.
| 개념 | 설명 |
|---|---|
| 3D Polar Angle | 위치를 (θ, φ, 거리)로 표현하는 각도 기반 좌표계 |
| Radian | 2D 원 위에서의 각도로, 호 길이와 반지름 비율로 정의됨 |
| Steradian | 3D 공간의 Solid Angle 단위로, 구의 면적 비율로 정의됨 |
| Radiant Intensity (J) | 단위 solid angle 당 방출되는 빛의 양 (W/sr) |
| Irradiance (E) | 단위 면적당 들어오는 빛의 양 (W/m²) |
| Radiance (L) | 특정 방향으로 반사되는 단위 면적·단위 각도당 빛의 양 (W/m²·sr) |
참고자료
Slide credit : Shree Nayar
https://www.youtube.com/@firstprinciplesofcomputerv3258/videos
