PnP 문제란 무엇인가?
이번 글에서는
Perspective n Point (PnP)
에 대하여 살펴보겠습니다.
Perspective n Point (PnP) 문제는
컴퓨터 비전과 로봇공학 분야에서
중요한 문제 중 하나로,
3차원 공간의 점들과
그 점들의 2차원 이미지 투영 사이의
관계를 이용해
카메라의 위치와 방향을
결정하는 과정입니다.
이 문제는 특히 증강 현실, 로봇 항법, 3D 재구성 등
다양한 응용 분야에서 필수적입니다.
위 설명만으로는 직관적으로
무슨 문제를 풀겠다는 건지
감이 안오므로 예시를 보겠습니다.

우리는 예전에 찍힌
사진들을 이용하여
이 사진이 어디에서
찍혔는지 찾아내곤 합니다.
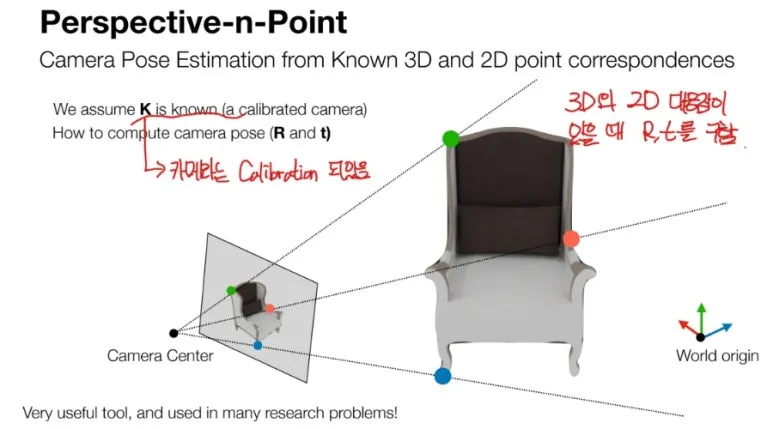
즉, 이 사진을 촬영할 때의
카메라의 위치와 포즈를 찾을 수 있습니다.
PnP 문제를 풀기 위한 사전 지식
들어가기 전에,
아래 내용을 모르시거나,
헷갈리시는 분들은
리마인드가 필요합니다.
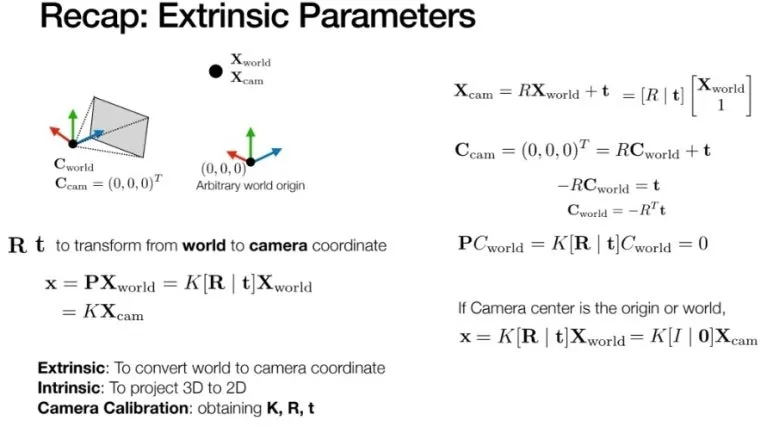
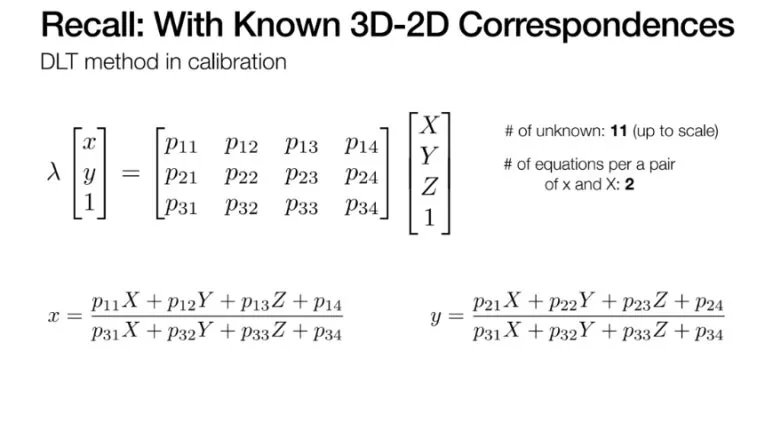

이미 살펴봤던 내용이므로,
한번씩 다시 보시면 도움이 됩니다.
PnP의 입력과 출력 구성
PnP 는 카메라의 위치와 포즈를
구하는 문제라고 했습니다.
우리가 문제를 풀면 P 를
구할 수 있게 되고
P 는 K,R,t 로 구성되어 있습니다.
문제를 풀기에 앞서서
Intrinsic parameters K 는
주어졌다고 가정하고 풀게됩니다.
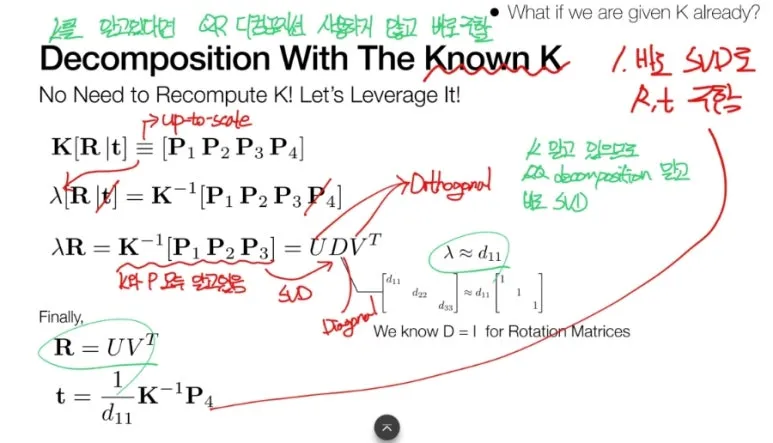
R,t 가 목적이니까요.
자, 그러면 이제 PnP 를
어떻게 푸는지 살펴보겠습니다.

P 는 3×4 matrix 입니다.
11 DoF 를 가지고 있습니다.
K 는 5 DoF 를 가지므로,
우리는 11-5 = 6 DoF 만 풀면 됩니다.
즉, 3개의 대응점이 필요합니다.
PnP 에서 n 은
Number of correspondence 를 의미합니다.
대응점의 수가 많을 수록
Robust 해지고,
Ransac 도 이용할 수 있으므로
많은게 좋을 것 같습니다.
6DoF 이므로 최소
3개는 필요하므로,
P3P 가 최소 대응점으로
문제를 푸는 방법입니다.
최소 대응점으로 푸는 P3P 방식
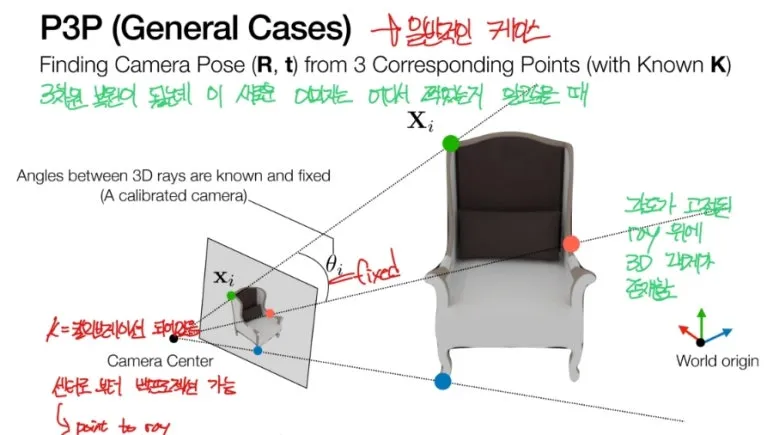
P3P 를 살펴보겠습니다.
2D 이미지에서 3개의 점과
그에 대응되는 3D 점을 찾습니다.
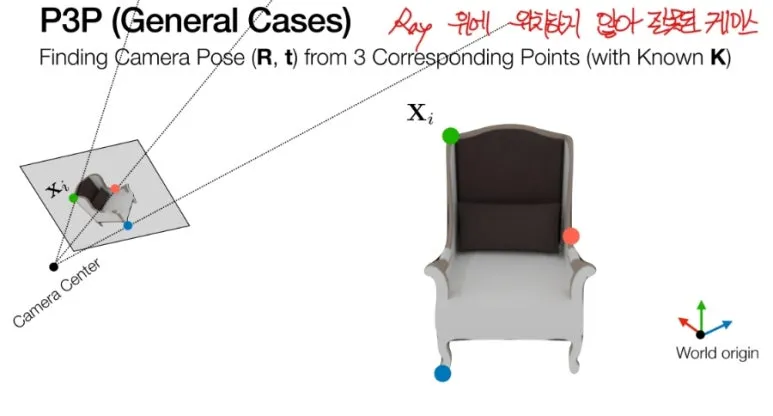
대응이 된다는 것은
동일 ray 위에 위치한다는
것을 의미합니다.
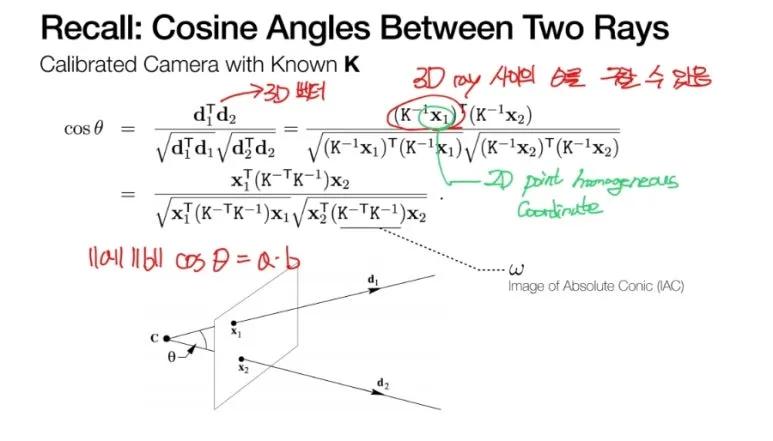
두 개의 벡터를 알면,
그 사이의 각도를 구할 수 있습니다.
이것을 이용해서 식을 풀어보겠습니다.
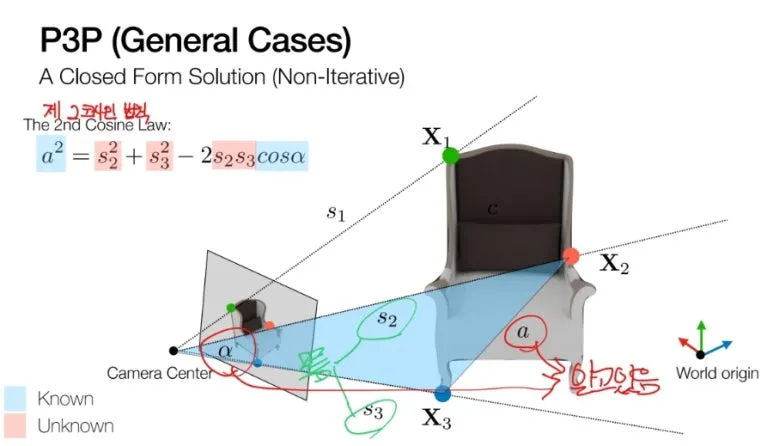
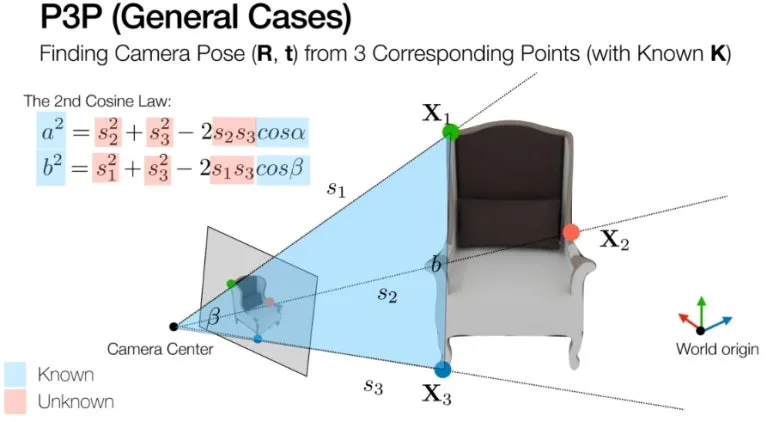
제 2 코사인 법칙으로
3개의 식을 만들어 냅니다.
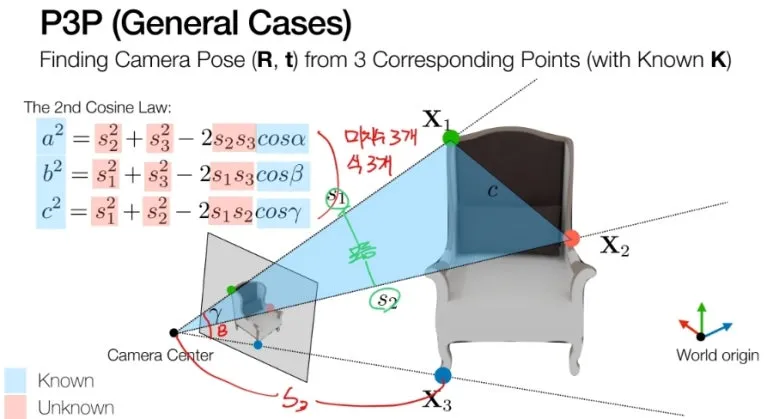
식 3개를 이용하여
미지수 3개를 구할 수 있습니다.

문제는 이 식을 풀기가
매우 복잡합니다.
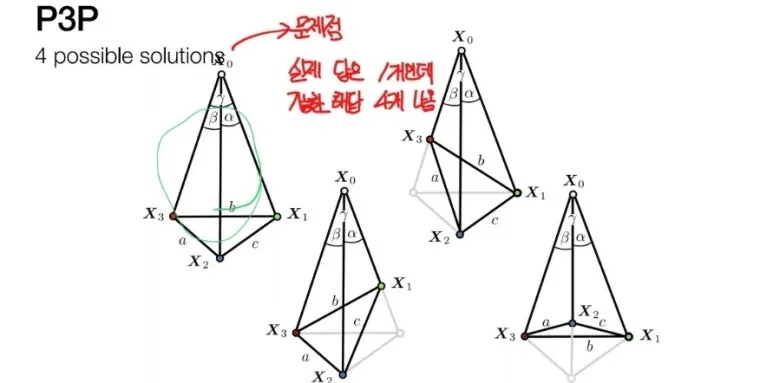
또한 풀었다고 하더라도,
4개의 가능한 해답이 나오고
이 중에서 실제 정답은
1개 뿐이라,
한번 더 확인이 필요합니다.
효율적인 방법: EPnP 알고리즘
우리는 대응점을
SIFT 와 같은 알고리즘을
이용하여 무수히 많이 추출합니다.
따라서,
실제로는 EPnP 같은
방식을 사용합니다.
여기서 E는 Efficient 의미를
가지고 있습니다.
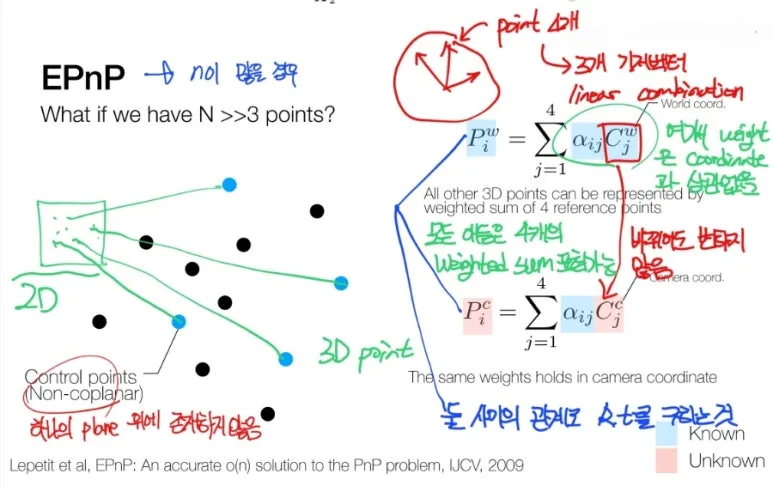
하나의 Plane 위에 위치하지 않는
4개의 Control points 를 뽑습니다.
그러면,
모든 점들을 선형 결합으로
표현 할 수 있습니다.
따라서 모든 점들을
4개의 Control points 를
이용하여 Weighted sum 으로
표현할 수 있습니다.
이렇게 생긴 weight 은 coordinate 이
변하더라도 바뀌지 않습니다.
Control points 들과
해당 점 사이의 관계이기 때문입니다.
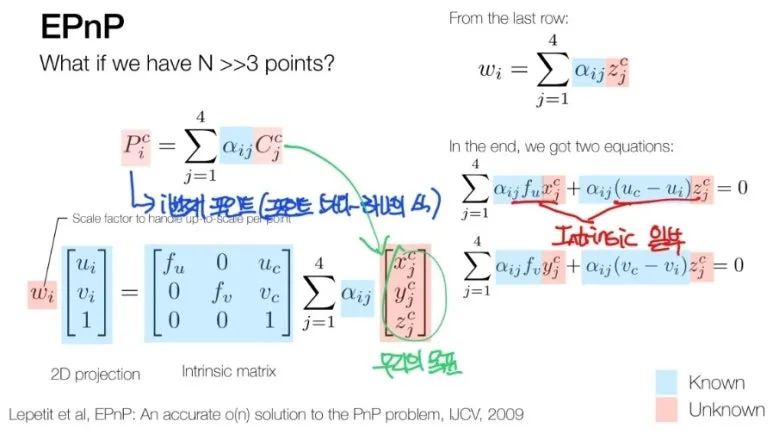
따라서 우리는 하나의 포인트마다
위와 같은 식을 만들 수 있습니다.
해당 식에서 맨 아랫줄
식을 먼저 구한 뒤,
식을 치환하여 2개의
식을 구할 수 있습니다.


즉, 정리하자면 Camera coordinate 에서
Control points 들을 알게되면
Camera coordinate 에서
모든 Point 들을 알게 됩니다.
이제, Camera coordinate 의 포인트들과
World coordinate 의 포인트들
사이의 R,t 를 구하면 됩니다.
RANSAC, 비선형 최적화 통합

OpenCV 에 잘 완성된 코드가 있습니다.
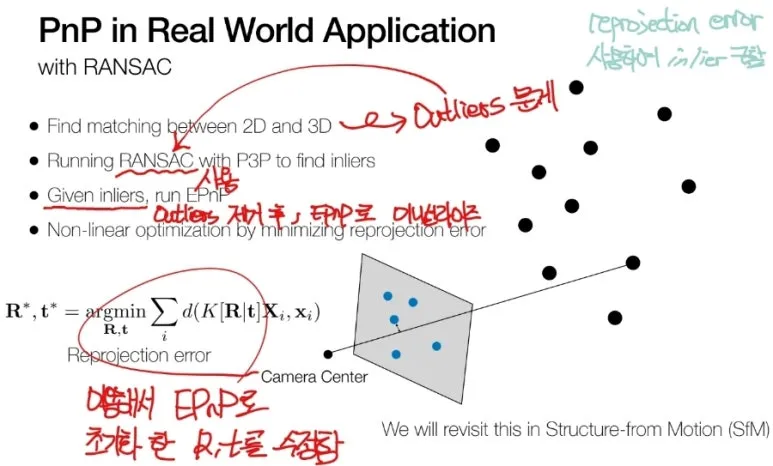
실제 사용할 때는 RANSAC 과정과
Non-linear optimization 과정을
반복적으로 묶어서
사용하게 됩니다.
| 항목 | P3P | EPnP |
|---|---|---|
| 의미 | Perspective-3-Point | Efficient Perspective-n-Point |
| 최소 대응점 수 | 3개 | 4개 이상 |
| 계산 방식 | 삼각법 기반 코사인 법칙 활용 | 4개 Control Points 기반 선형 결합 사용 |
| 계산 복잡도 | 비선형, 해가 최대 4개까지 존재 가능 | 선형화 + 효율적 계산 |
| 실제 적용 여부 | 거의 사용되지 않음 (이론적 방법) | OpenCV 등에서 실제로 많이 사용 |
| RANSAC 사용 | 필요 | 필수 (Outlier 제거 + Robust 추정) |
그런 건 난 잘 모르겠고,
PnP 는 카메라 위치와 방향
구하는 알고리즘
참고자료
Slide credit : Joo Hanbyul
https://homes.cs.washington.edu/~seitz/talks/3Dhistory.pdf
