RANSAC 이란?
이번 글에서는
RANSAC (Random Sample Consensus)
에 대하여 살펴보겠습니다.
우리는 투영된 공간에서
2차원 Plane 의 변환을 구하기 위해서
대응점 (Correspondences) 을 찾아서
DLT 를 이용하여 문제를
푸는 것을 살펴봤었습니다.
그런데,
여기서 우리가 찾는 대응점이
정말 일치하는 대응점일까요?

대응점은 보통 descrptors 이용하여
컴퓨터가 자동으로 찾게 합니다.
이 과정을
Feature extraction
(특징점 추출) 이라고도 합니다.
가장 유명한 SIFT 가
대표적인 예가 되겠습니다.

이렇게 찾은 대응점이 정말 정확할까요?
사진에는 하늘, 잔디,나무 와
같은 장면들도 찍힙니다.
SIFT 가 굉장히 좋은 성능을 가지지만,
실제 물리적으로 유사한 부분들이
세상에 너무나도 많이 존재합니다.

따라서,
우리는 Outliers (이상치) 제거를
해줘야 합니다.
이 때 사용하는 대표적인
방법론이 RANSAC 입니다.
RANSAC 알고리즘의 동작 원리
RANSAC 의 작동 원리를
살펴보겠습니다.
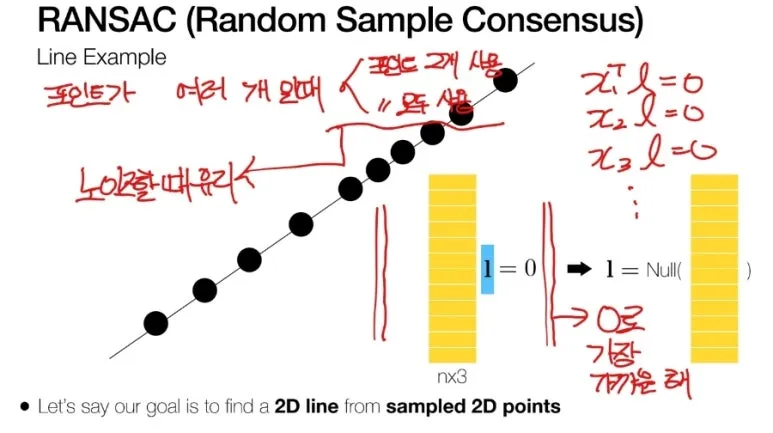
여기서 Line 위에 존재하는
Point 들은 Inliers 입니다.
Line 밖에 존재하는
Point 들은 Outliers 입니다.
정말 이상적이게 점들이
모두 라인 위에 존재하면 좋겠지만,
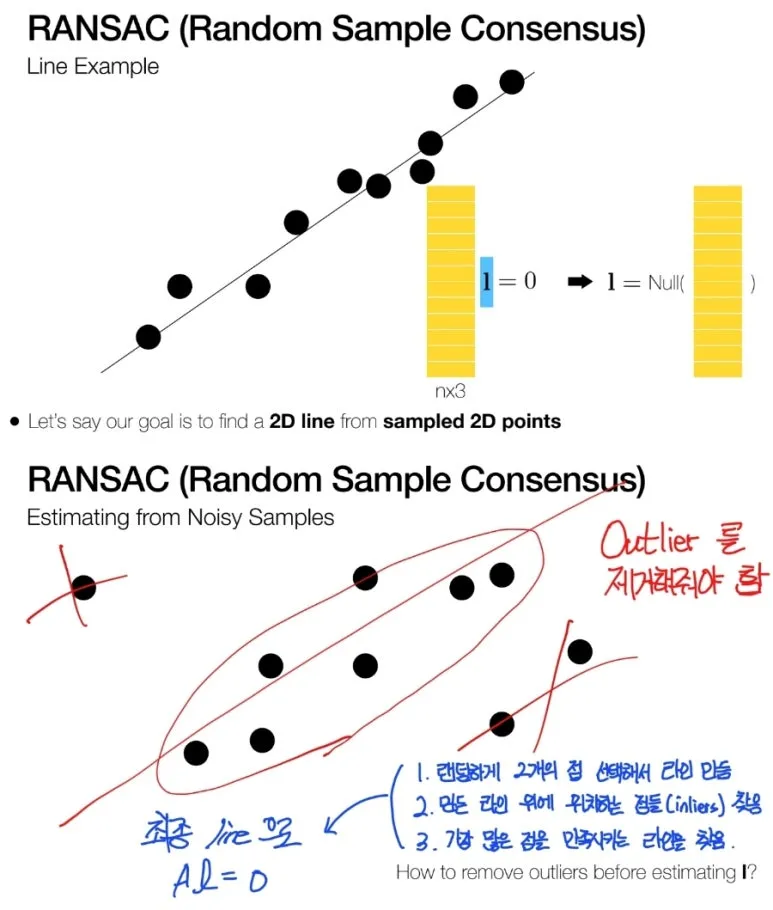
현실은 다릅니다.
점들이 사방으로 퍼져 있습니다.
노이즈와 이상치 등이
섞여있기 때문입니다.
가장 적합한 Line 을 찾아보겠습니다.
1. 2개의 점을 임의로 선택하여 라인을 만든다.
2. 해당 라인 위에 위치하는 점들의 개수를 카운트한다.
3. 이렇게 여러 라인을 테스트 해본다.
4. 가장 많은 점을 가지는 라인을 최종 선택한다.
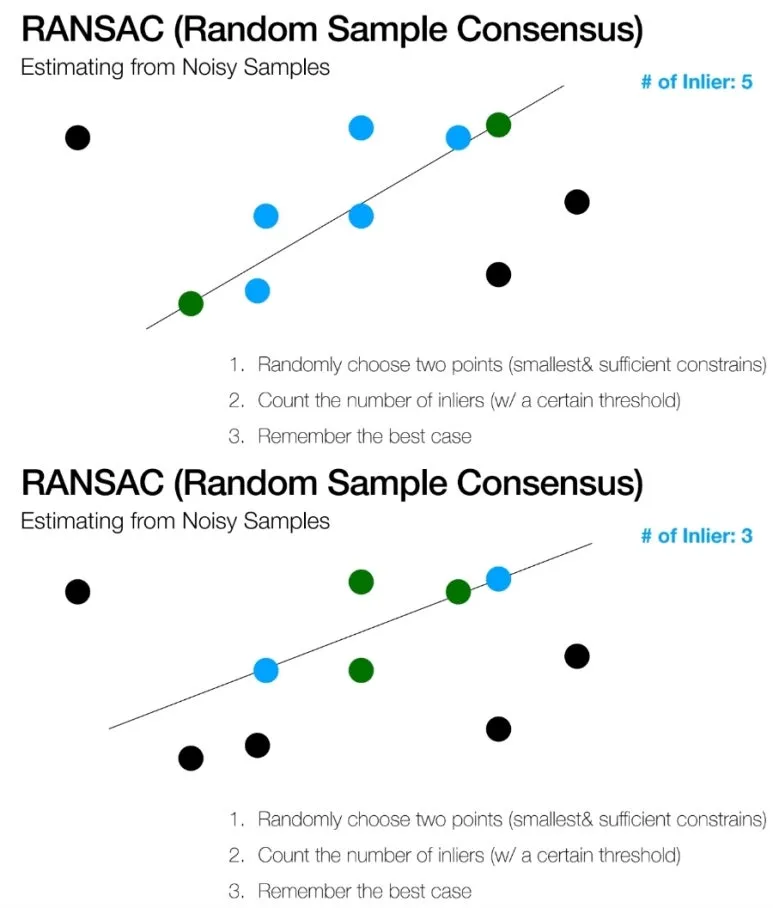
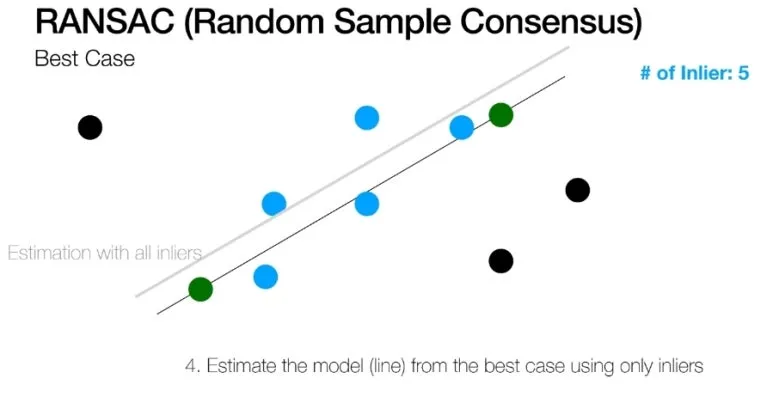
이렇게 선택한 라인에 위치하지
못하는 점들은 이상치라고
가정할 수 있습니다.

이렇게 반복적으로 작업을 하다 보니,
Outliers 가 많아지면 속도가
많이 느려지게 됩니다.

3D vision 을 하다보면,
매 Step 마다 RANSAC 을 진행하기도 합니다.
경험적인 방법이다 보니,
반복적으로 작업을 해야해서 느리고,
Guarantee 가 없다는 단점도 있습니다.
| 항목 | 설명 |
|---|---|
| 목적 | 이상치(Outlier)를 제거해 신뢰할 수 있는 모델 추정 |
| 적용 대상 | Homography, 선형 회귀, PnP 등 다양한 모델 추정에 사용 |
| 입력 | 전체 대응점 집합 (Inliers + Outliers 포함) |
| 반복 절차 | 임의 샘플 → 모델 추정 → 일치 수 평가 → 최고 모델 선택 |
| 핵심 평가 기준 | 모델 위에 잘 맞는 점 (Inliers) 개수 |
| 장점 | 강건함 (노이즈/이상치에 강함) |
| 단점 | 반복 횟수가 많아 계산 비용 큼, 항상 정답을 보장하지는 않음 |
| 후처리 | DLT 및 Non-linear optimization 으로 정밀한 Homography 개선 가능 |

이렇게 RANSAC 을 이용하여
이상치를 제거한 대응점들을
이용하여 DLT 를 사용한다면
Homography 를 쉽게 찾을 수 있습니다.
DLT 가 Algebraic 한 방법이라,
Geometric error 를 제거하기 위해
Non-linear optimization 을
추가로 진행하기도 합니다.
이것에 대해서는 다음에 알아보겠습니다.
그런 건 난 잘 모르겠고,
RANSAC 은 이상치 제거를
위한 대표적 방법
참고자료
Slide credit : Joo Hanbyul
https://homes.cs.washington.edu/~seitz/talks/3Dhistory.pdf
