카메라 캘리브레이션이란?
이번 글에서는
Calibration
에 대해서 살펴보겠습니다.

Calibration 이란
Camera parameter (= P) 를
구하는 것을 의미합니다.
P는 K,R,t 로 분해할 수 있으니,
K,R,t 를 구한다고 생각하셔도 동일합니다.
여러가지 방법이 있지만,
우리는 DLT 를 이용한 방법과
Zhang’s method 를 살펴보겠습니다.
DLT를 활용한 Calibration 방법
이전에 DLT 를 다룬 적이 있습니다.
대응점을 찾아 수식을
푸는 방법이였습니다.

DLT 를 이용하여
Calibration 을 하기 위해서는
실제 크기를 알고 있는
3D 객체가 필요합니다.
그리고 이 객체를 촬영하여
이미지를 만듭니다.
우리는 World coordinate 의 origin 을
객체 위에 두고 실제
알고 있는 크기를 (=물리적 크기)
이용하여 특정 위치가
어떠한 값을 갖는지
구할 수 있습니다.
이와 동일한 위치를
2D 이미지 위에서
(x,y) 좌표를 구할 수 있습니다.
이 2개가 한 쌍의
대응점이 됩니다.

여러 개의 대응점을 구했다면,
우리는 DLT 를 사용할 수 있습니다.

소문자 x 는 2D 이미지 좌표이고,
대문자 x는 3D 객체의 좌표입니다.
3D 위치를 Camera parameter (=P) 를
곱해서 projection 시키면
2D 위치를 계산할 수 있습니다.

P 는 3×4 matrix 이므로,
12 DoF 를 갖지만,
Up to scale 이므로 -1 하여
11 DoF 입니다.
우리는 최소 6쌍의 대응점이
필요하다는 것을 알 수 있습니다.

물론 많으면 많을수록
강인한 결과를 얻을 수 있습니다.
여기서 강인하다는 뜻은,
어떠한 대응점을 가져와도
왠만하면 만족한다는 뜻 입니다.

하지만, 실제로 3D 객체를
준비하는 과정은
정해진 규격으로 제작을 해야 되는
매우 번거로운 일입니다.
Zhang’s Method란?

Zhang’s Method 는 체크보드를
다양하게 찍어 Calibration 을 진행합니다.

체크보드란 위와 같은 특징을
가진 2D plane 을 의미하며,
컴퓨터가 쉽게 corner 혹은
center 를 탐지할 수 있습니다.

여기서도 마찬가지로
임의의 World coordinate 에서
depth 를 0 으로 고정 시킨 후
특정 위치의 좌표 값을
얻어낼 수 있습니다.
우리는 실제 체크보드의 크기를 알고 있고
Origin 을 2D plane 위에 두었을 때
depth 는 모두 0으로
동일하기 때문입니다.

Depth value 가 0으로 고정이므로
우리는 이 부분을 삭제하여
Homography 관계의 식을
만들 수 있습니다.
3×3 matrix 는 8 DoF 이므로
4개의 대응점으로
풀 수 있습니다.

이렇게 구한 Homography 를
바로 분해할 수는 없고,
Rotation matrix 의
성질을 이용하여
여러 식을 거쳐서
분해할 수 있습니다.

B 를 구해야 하는데 Symmetric 이므로
5 DoF 가 됩니다.
따라서,
우리는 최소 다양한 각도로
찍힌 체크보드 사진이
3장은 필요합니다.
(= 3개의 Homography 필요)

보통 Zhangs method 는
단일 카메라의 시스템의
Calibration 에 많이 사용됩니다.
찍힌 이미지가 모두
동일한 K 파라미터를
가지고 있다고
가정하기 때문입니다.

이렇게 K를 알아냈다면,
단순 계산을 이용하여
R,t 도 구할 수 있습니다.
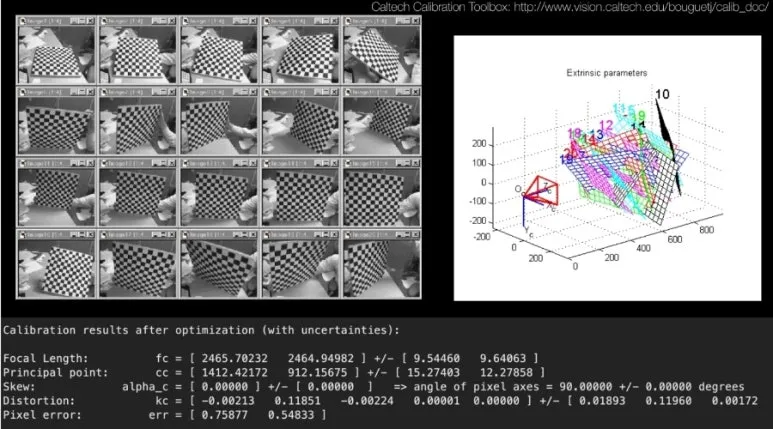
수식적으로는 여러 과정을
거쳐야되서 많이 복잡하지만,
자주 사용되기 때문에
이미 잘 완성된 코드들이
많이 있습니다.
가장 자주 쓰이는 Calibration 방법은
SfM (Structure from Motion) 으로,
COLMAP 을 사용합니다.
이건 나중에 따로 다루겠습니다.
| 항목 | DLT 방식 | Zhang’s Method |
|---|---|---|
| 요구 데이터 | 3D 객체의 실제 좌표 + 2D 이미지 좌표 | 체크보드 이미지 여러 장 |
| 대응점 개수 | 최소 6쌍 (12 unknowns → 11 DoF) | 각 이미지마다 최소 4쌍 (Homography는 8 DoF) |
| Depth 정보 필요 여부 | 3D 위치 정보 필요 | Depth=0 (2D Plane 가정) |
| 수학적 원리 | P 행렬 직접 계산 후 분해 | Homography → K → R,t 분해 |
| 장점 | 기하학적으로 직관적 | 장비 없이 쉽게 수행 가능 |
| 단점 | 3D 객체 필요, 구축 어려움 | 다양한 각도에서 다수의 촬영 필요 |
| 사용 용도 | 고정된 3D 환경에서 정확한 모델링 | 일반적인 단일 카메라 캘리브레이션에 널리 사용 |
| 대표 활용 툴 | OpenCV, MATLAB 등 | OpenCV, COLMAP 등 |
그런 건 난 잘 모르겠고,
Calibration 이란
카메라 파라미터 K,R,t (=P) 를
계산하는 것
참고자료
Slide credit : Joo Hanbyul
