유클리드 기하학(Euclidean Geometry)란?
이번 글에서는
Euclidean Geometry VS Projective Geometry
에 대해서 비교하며 살펴보겠습니다.
우리가 3D 를 공부하기 위해서는
공간에 대한 개념을
이해하는 것이 중요합니다.
우선 Euclidean Geometry (유클리드 기하학)
을 살펴보겠습니다.
Euclidean space 에 대해
살펴본 적이 있습니다.

정확히 동일하게 우리가
살고있는 3D 세상을 의미합니다.

그런데 문제가 있습니다.
Euclidean geometry 에서는
Infinity 를 정의하지 않습니다.
소실점(Vanishing Point) 이란?

Infinity point 란
Vanishing point 라고 부르기도 합니다.
그림에서 보면 도로가 정말 길게 쭉
뻗어져 있는 것을 촬영했습니다.
우리는 길이 끊기지 않고 뻗어있는 것을
알고있는데 사진에서는
한 점으로 모이게 됩니다.
이것이 Vanishing point (= 소실점) 입니다.
평행한 선들이 만나는 점 입니다.
이 점은 Euclidean Geometry
에서는 정의되지 않으며,
Projective Geometry 에서
표현할 수 있습니다.
사영 기하학(Projective Geometry)란?

Projective Geometry 는 간단하게 말해서
Euclidean 에서 Infinity Points 개념을
추가한 공간이라고 볼 수 있습니다.
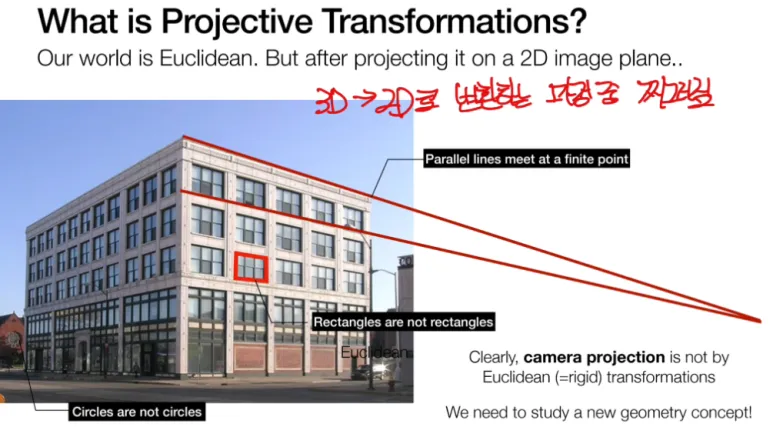
우리가 사진을 찍기 위해
카메라를 통하여 본 세상이,
Projective Geometry 라고 이해해 볼 수 있습니다.
| 구분 | Euclidean Geometry (유클리드 기하학) | Projective Geometry (사영 기하학) |
|---|---|---|
| 정의 | 현실 세계의 3차원 공간을 수학적으로 표현 | 카메라 이미지 공간(투영된 세계) 표현 |
| 소실점 개념 | 없음 (무한대 정의 불가) | 있음 (Vanishing point 표현 가능) |
| 직선의 평행성 | 평행선은 평생 만나지 않음 | 평행선은 무한대에서 만남 |
| 응용 분야 | 전통 기하학, 공학, CAD | 컴퓨터 비전, 카메라 모델, 3D 복원 |
| 핵심 개념 | 거리, 각도 보존 | 투영, 무한대 점 개념 포함 |
그런 건 난 잘 모르겠고,
Euclidean Geometry = 실제 세상
Projective Geometry = 카메라를 통해 본 세상
참고자료
Slide credit : Joo Hanbyul
https://homes.cs.washington.edu/~seitz/talks/3Dhistory.pdf
