선형대수학의 모든 주제는
벡터의 덧셈과 상수배를
중심으로 이루어집니다.
Addition (덧셈)
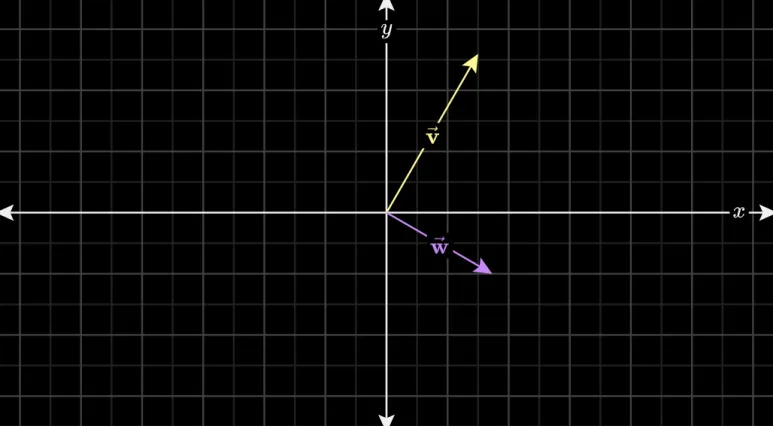
두 벡터 v 와 w 가 있습니다.
이 두 벡터를 어떻게 더할까요?
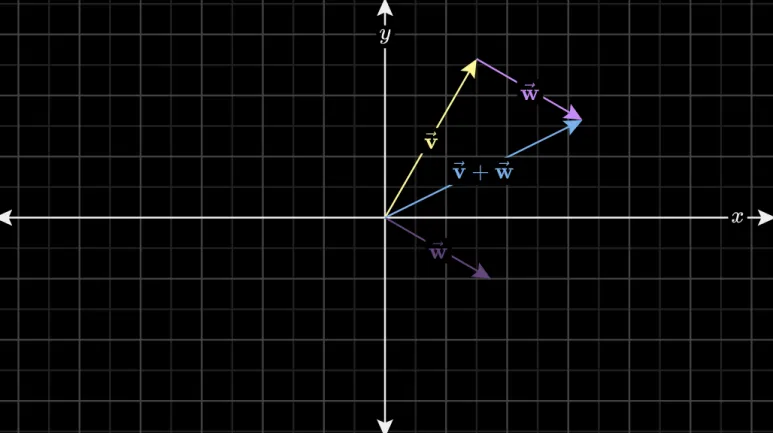
벡터 w 를 움직여서 꼬리부분을
벡터 v 의 머리 부분으로 이동시킵니다.
벡터 v의 꼬리 부분에서 시작해서
벡터 w의 머리 부분으로 향하는
새로운 벡터를 그리면
이것이 두 벡터의 합입니다.
갑자기 w 의 벡터를 움직여서 어디다 붙이고
저는 잘 이해가 가지 않았습니다.
결과적으로 보면,
2차원 상의 벡터는 x,y 축으로의
움직임을 나타냅니다.
v벡터의 x,y 만큼 움직여서
도착한 위치에서
다시 w 벡터의 x,y 만큼 움직여서
도착한 위치는
두 벡터의 합으로 만들어진
새로운 벡터의 x,y 만큼 이동한 값과
같은 위치에 도착하게 됩니다.

이러한 방법은 우리가 덧셈을 처음
어린이들에게 가르칠 때,
수직선 위에서 2+5 는 7 이라고
알려주는 방법과 동일합니다.
즉, 수직선 위의 숫자를 더하는
과정의 확장이라고 볼 수도 있습니다.
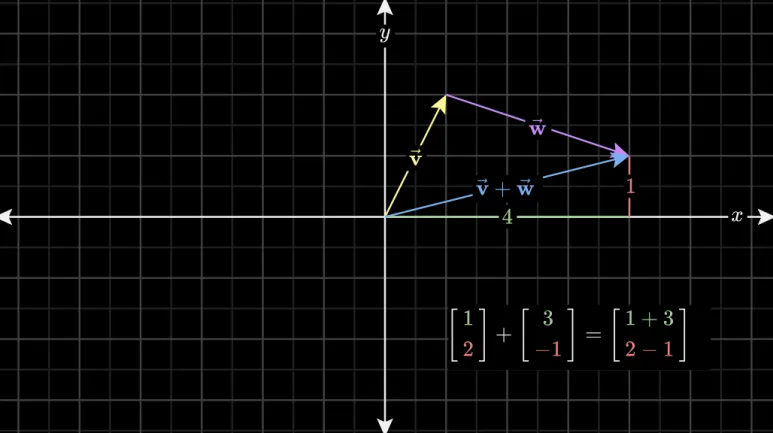
두 벡터의 합의 좌표를 구하는 것은
두 벡터의 각 항들을 매치시킨 후
더하는 것과 같습니다.
Scaling (상수배)
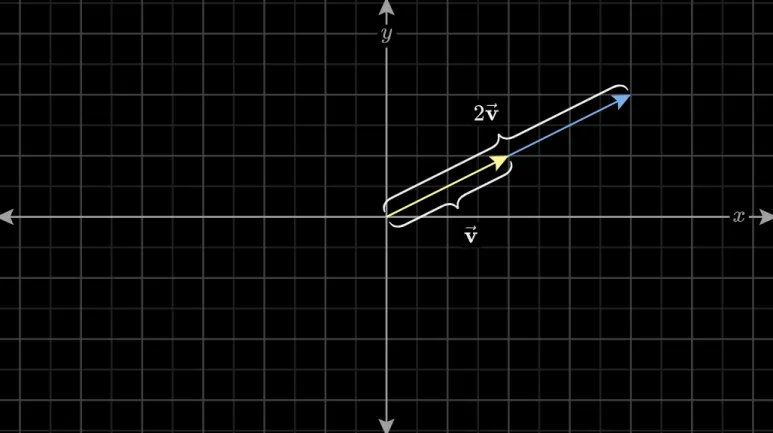
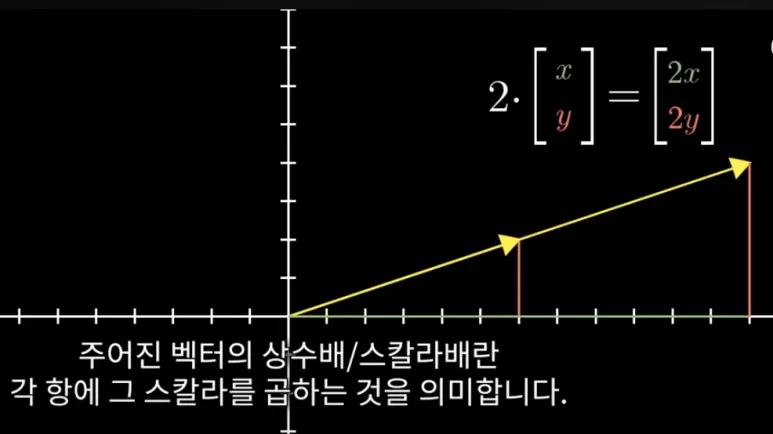
주어진 벡터에 2를 곱한다면,
그 벡터는 처음 길이의
두 배 만큼 늘어나게 됩니다.
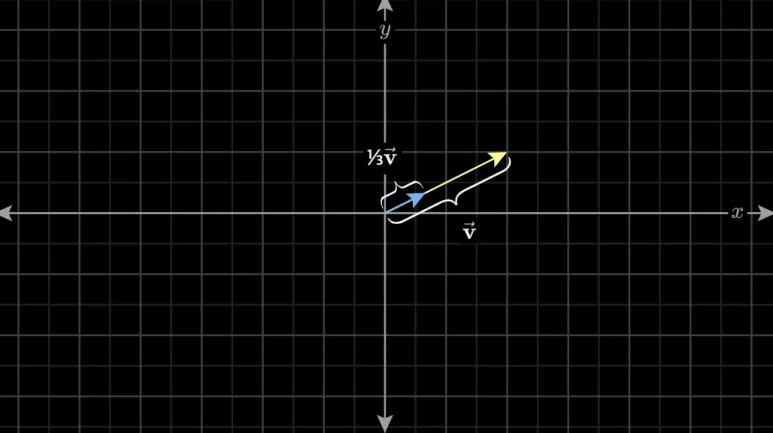
1/3 을 곱한다면 처음 길이의
1/3 으로 줄어들게 됩니다.
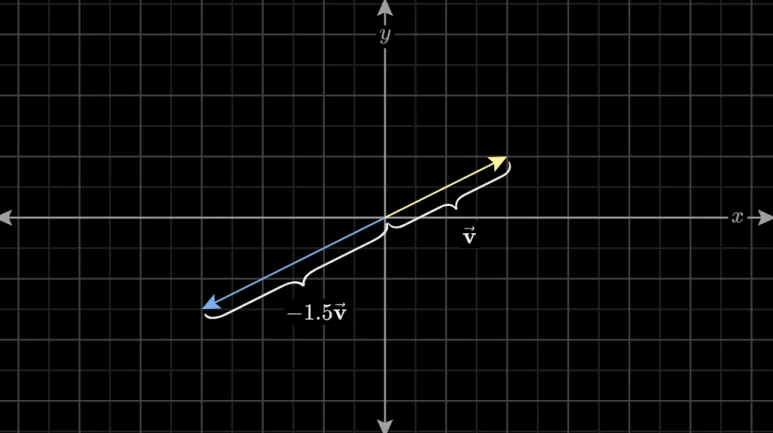
만약 -1.8 음수를 곱한다면,
벡터를 뒤집은 후,
처음 길이의 1.8배만큼 늘어나게 됩니다.
즉, Scaling (상수배) 란 원래의 벡터의
방향은 유지한 채 길이를 늘이고 줄이고
뒤집는 과정을 의미합니다.
벡터를 상수배하는 숫자, 2,1/3
그리고 -1.8 같은 숫자를
Scalar(스칼라) 라고 합니다.
선형대수학 전체에서 숫자들의
주된 역활이 바로 벡터를
스케일하는 것이라
스칼라를 숫자와 같은 의미로
사용하기도 합니다.
참고자료
https://www.3blue1brown.com/lessons/vectors
https://www.youtube.com/watch?list=PLkoaXOTFHiqhVDo0nWybNmihCP_4BjOFR&v=ArgTeYVuJUo&embeds_referring_euri=https%3A%2F%2Fblog.naver.com%2F&source_ve_path=MjM4NTEource_ve_path=MjM4NTE
